Общая информация:
Авторы: Александр Бронников, Ольга Бронникова, Нигина Шаропова
Для цитаты: Бронников А., Бронникова О., Шаропова Н. Полярность означающего // Лакан-Паук. № 1/2. 2022. С. 53-77.
Текст статьи в формате pdf:
Текст:
Содержание
- Реальное Лакана
- От инволюции к полярности
- Определение полярности
- Первая интерпретация, или Как от геометрии перейти к психоанализу
- Первая иллюстрация, в которой полярность предстаёт как инволюция между метафорой и метонимией
- Геометрия метафоры
- О влечениях и конических сечениях
- Пересекая горизонт
- Несколько слов о кросс-кэпе
- Завершение
Полярность означающего
Автором этого текста можно смело назвать коллектив из трёх человек, который потратил какую-то часть своей жизни на картель по вопросам связи психоанализа и проективной геометрии. Поэтому этот текст, хотя и написан одним из трёх, но в целом держится скорее как борромеев узел: любое из колец можно рассматривать как то, без чего всё распалось бы. Картель проходил летом 2019 года, его участниками были Ольга Бронникова, Нигина Шаропова, Александр Бронников.
Реальное Лакана и горизонт Дезарга
Самую простую иллюстрацию того, чем является регистр Реального, Лакан давал на примере множества натуральных чисел. Заключается эта арифметическая иллюстрация в том факте, что самого большого натурального числа не существует. Этот пример связывает Реальное с модальностью невозможного.
Геометрической вариацией иллюстрации этого невозможного является, например, точка пересечения параллельных прямых. Психоаналитической иллюстрацией являются, например, проблемы принятия женственности, которые Фрейд обсуждает в работе Анализ конечный и бесконечный.
В этом тексте мы, в основном, будем говорить именно о геометрической вариации.
Наша философская позиция по отношению к регистру Реального совпадает с позицией Яаакко Хинтикки, которую он озвучил в тексте о проблемах определения истины и которую можно резюмировать своего рода девизом из работы Вапперо: «То, о чём невозможно сказать, стоит попробовать записать». Можно вспомнить и самого Лакана, который, например, в своих
формулах сексуации под модальностью невозможного (то, что не перестаёт не записываться) пишет случайное (то, что перестаёт не записываться). Этот переход от «не перестаёт не записываться» к «перестаёт не записываться» является своего рода визитной карточкой, ну, или ключом к пониманию того, как читает Лакана Ж.-М. Вапперо. Кажется, что если бы не его работы, то лакановское учение было бы обречено на регресс к достаточно банальным идеям о чём-то всегда несхватываемом, ускользающем от означающего, о такой вечно недоступной пуповине сновидения, которой иллюстрируют Реальное и которую молниеносно фетишизируют, в пределе делая психоаналитический дискурс разновидностью культа невыразимого.
Озвученный в лакановских терминах переход от невозможного к случайному подразумевает прежде всего именно переход, то есть некоторую трансформацию. Проще говоря, он ставит вопрос о том, что, собственно, с этим Реальным случается на психоанализе? Его мы предлагаем держать в уме, когда будем говорить о том, что назвали геометрической
вариацией иллюстрации Реального.
Как мы и сказали, состоит эта геометрическая вариация в том, что в геометрии имеют место параллельные прямые. Две «обычные» прямые пересекаются или задают точку (точку пересечения), а вот параллельные прямые этого не делают. Они не вступают в отношения, которые мы назвали пересечением. Однако в геометрии, первоначально благодаря Дезаргу, происходит трансформация, касающаяся этой несуществующей точки. Из несуществующей точки она превращается в мнимую. Появляется множество мнимых точек пересечения параллельных прямых. Оно получает имя горизонта, прямой на бесконечности, недоступной прямой, или (в лакановских терминах) становится линией без точек.
Другими словами, в геометрии мы переходим от точки, которая не существует, к точке, которая имеет место, но мы не знаем где (ex-sistence). Так появляются задачи на построение с недоступными элементами, то есть предлагается нечто нарисовать, но теперь с учётом наличия мнимой прямой, ну, или недоступного горизонта. Горизонт действительно становится прямой, но такой, до которой, говоря несколько неформально, не доехать по рельсам движений евклидовой геометрии1. Тем не менее, теперь, когда от несуществующей прямой мы перешли к прямой мнимой, у нас, как мы покажем в этой работе, появляется инструмент, делающий доступной запись через евклидовы движения того, чего ранее они не писали и что в некотором смысле можно назвать движением, которое «пересекает» недоступный горизонт.
Этот инструмент прямо отсылает к понятию инволюции, которое Лакан заимствовал у Дезарга, вводя в оборот выражение «инволюция означающего». Последнее Вапперо назвал инвариантом лакановского учения: о каком бы Лакане ни шла речь (о раннем, позднем или совсем позднем), каким бы топологическим материалом он бы ни пользовался (графами, поверхностями, узлами), согласно Вапперо, инволюция означающего является тем, что сохраняется на всех этапах и во всех формах записи.
Наша идея состоит, таким образом, в том, чтобы увидеть, каким образом эта инволюция имеет дело с Реальным. Ну, или можно усилить тезис, сказав, что наша гипотеза как раз и заключается в том, что инволюция означающего — это и есть ответ на вопрос, что, собственно, с этим Реальным делать2.
Мы увидим, что инволюция у Лакана — это такой своего рода психоаналитический аналог формулы мифической трансформации Леви-Стросса, формулы, про которую сам Лакан говорил, что она связана с Реальным мифа. Прежде всего, тут уместно напомнить, что миф, согласно Леви-Строссу, схватывается через его трансформацию. Её пишет эта формула, сопоставляя между собой две различные версии одного и того же мифа (тождество различного). При этом миф, который определяется через его трансформацию, образуется на месте вопроса, прямой ответ на который представляется затруднительным, ну, или, в пределе, невозможным. Другими словами, в его основе лежит то, что отсылает к регистру Реального.
От инволюции к полярности
Нам кажется продуктивным не только обращение к проективной геометрии, из которой был заимствован термин «инволюция», но и переход от этого термина к термину, который не звучал у Лакана эксплицитно, а именно — к термину полярность. Мы можем мотивировать эту замену несколькими аргументами, в том числе и тем, что, хотя у Лакана слово «полярность» не используется явно, в семинаре Объект психоанализа, когда он говорит о принципе дуальности в геометрии Дезарга, он использует материал, который к этому термину совершенно непосредственно отсылает. С другой стороны, мотив введения нового понятия можно объяснить не только через цитату, но и через само его содержание, которое, как мы покажем, эффективно работает в областях, близких психоаналитическому дискурсу.
Но прежде, чем показать эту эффективность, укажем на существующие заимствования материала из проективной геометрии в работах Лакана и Вапперо.
С одной стороны, у Дезарга Лакан взял идею завершения бесконечной прямой, когда, например, в XXIII семинаре рисовал узел сначала прямыми, а потом завершал их, превращая в окружности. Другими словами, снабжал их тем, что выше мы назвали точкой на бесконечности. У Вапперо точка на бесконечности, завершающая прямую, стала вариацией записи объекта малое а.
С другой стороны, имеет место понятие инволюции, которое, к примеру, у того же Вапперо получило связь с нарциссизмом.
Если попробовать в двух словах пересказать его работу, то прежде всего Вапперо отмечает, что нарциссизм, по определению Фрейда, — это отношение к себе самому как к сексуальному объекту. Но что значит отнестись к себе как к объекту? Стадия зеркала Жака Лакана говорит нам, что это удвоение «к себе самому в качестве объекта» иллюстрирует зеркальное отражение, потому что человек, который смотрит на себя в зеркало, одновременно является и тем, кто смотрит, и тем объектом, который предстаёт в зеркале среди других объектов типа шкаф, диван и т. д. Это одновременно один и тот же человек, но есть отличие: он является и тем, кто смотрит, и тем, на кого смотрят. Поэтому, говорит Вапперо, нарциссизм позволяет существование пары, которая объединяет идентичное с различным. Интренсек, или внутренне идентичные объекты (смотрящий и тот, кто отражается), отличаются экстренсек, или исходя из того, как они расположены в пространстве.
Инволюция в этой работе Вапперо рассматривается как инволютивная функция f2 = 1, примером которой является отражение или симметрия. Если f2 = 1, то f = f-1, другими словами, функция тождественна обратной к ней, откуда и возникает выражение «тождество различного». Вапперо показывает, что трёхмерный объект не тождественен своему зеркальному отражению.
Но отражение отражения (f2) возвращает нас в исходную точку. Всё это является его комментарием к фрейдовской паре я-либидо/объект-либидо» и позволяет лучше понять замечание Фрейда о том, что либидо, конечно, два, но, возможно, речь идёт о том же самом.
Итак, с одной стороны, из проективной геометрии к нам попадает завершение бесконечной прямой, коррелирующая с этим идея горизонта (горизонт=завершение плоскости), а с другой — инволютивная функция, то есть функция, повторное применение которой возвращает в начальную точку. Однако связь между этими двумя заимствованиями не очевидна. Кроме того,
в качестве инволютивной функции берётся симметрия, что, с одной стороны, естественно для исследования зеркала, но, с другой стороны, симметрия — это преобразование евклидовой геометрии, ну, или частный случай инволюции, которым можно заниматься совершенно без обращения к геометрии проективной. Таким образом, симметрия не позволяет явным образом увязать друг с другом идею завершения, или горизонта с инволюцией просто хотя бы потому, что симметрия рассматривается в евклидовом, ну, или незавершённом пространстве. Напротив, полярность, которая, как и симметрия, является разновидностью инволюции, гораздо лучше и нагляднее увязывает между собой идею линии на бесконечности и идею
тождества различного.
Определение полярности
Прежде всего скажем, что мы будем иметь дело с объектами на проективной плоскости. Интуитивно можно отличать её от евклидовой плоскости наличием горизонта, или линии на бесконечности. Если говорить точнее, то любые две прямые проективной плоскости пересекаются, даже те, что были на евклидовой плоскости параллельными, теперь тоже пересекутся, точка их пересечения будет лежать на горизонте. Короче говоря, мы находимся в мире, где удалось заменить одно означающее («прямые параллельны») на другое означающее («прямые пересекаются в точке на бесконечности»), и мы будем заниматься тем, что связано с эффектами этой замены. В этом мире, как выразился Лакан, между прямыми и точками возникает символическое тождество. Например, любые две точки задают прямую, и наоборот, любые две прямые задают точку. Как мы уже можем почувствовать, между прямыми и точками имеет место инволюция.
Полярность — это функция, которая переводит точки в прямые, а прямые — в точки, ну, или ставит в соответствие каждой точке плоскости прямую этой плоскости.
Чтобы задать такую функцию, нужно точно указать, как переводить точки в прямые и наоборот.
Благодаря проективной геометрии мы действительно получаем такое указание: любое коническое сечение (окружность, эллипс, парабола, гипербола) задаёт инволюцию, причём только одну, которая ставит в соответствие каждой точке плоскости прямую.
Рассмотрим окружность S. Возьмём произвольную точку А, лежащую вне этой окружности. Назовём её полюсом. Прямую а, которая будет ей соответствовать, назовём полярой. Построим эту прямую следующим образом. Из точки А проведём две касательные к окружности S и через две точки касания проведём а.

рис. 1. Полярность между точкой A и прямой а.
Если А — это точка на бесконечности, то её полярой окажется диаметр окружности. Это так, потому что две касательные к S, которые пересекаются на бесконечности (в А), будут параллельными линиями, а значит если соединить их точки касания, то получим диаметр окружности S.

рис. 2. Точка А лежит на горизонте. Касательные, проведенные из нее к окружности S, будут параллельными. Поэтому прямая а пройдёт через центр окружности.
Остаётся построить поляры внутренних точек окружности. Возьмём произвольную внутреннюю точку B. Проведём через неё две произвольные хорды (m, n), затем построим два полюса этих хорд (M, N), осуществив процедуру, обратную описанной выше. Другими словами, чтобы найти полюс хорды, нужно в точках, где она пересекает окружность, нарисовать касательные, и они пересекутся в полюсе, полярой которого эта хорда является. Затем проведём прямую МN, которая и будет искомой полярой точки B.

рис. 3.
В частности, центру конического сечения будет соответствовать прямая на бесконечности. Это можно понять по тому, что хорды (m, n) будут диаметрами, значит, касательные к точкам, в которых эти хорды пересекут S, будут параллельными, но тогда M и N окажутся точками на бесконечности, а прямая MN будет прямой на бесконечности.

рис. 4
Остаётся добавить, что точки самой окружности перейдут в прямые, которые касаются окружности в этих точках. Такие элементы называют самосопряжёнными.

рис. 5. Точка окружности А (полюс) и касательная а (поляра) называются самосопряжёнными.
Итак, коническое сечение S определило инволютивную функцию, которая переводит каждую точку плоскости в некоторую прямую этой плоскости. И, в частности, переводит действительную точку O1 (центр S) в недоступную прямую. В силу этого коническое сечение называют ядром полярности, ну, или просто используют одно и то же обозначение и для конического сечения, и для полярности, которую она задаёт.
Первая интерпретация, или Как от геометрии перейти к психоанализу
Один из путей перевода геометрического материала в психоаналитический дискурс опосредован работой Р. Якобсона о двух типах афазии. Принципиальным пунктом этой работы является различение синхронии и диахронии, которое приводит к различию метафоры и метонимии.
Для нашего перевода можно воспользоваться примечательным совпадением геометрических терминов и тех, что мы встречаем у Якобсона: речь идёт об оппозиции ряд/пучок, которую можно встретить в его тексте:
1) когда он говорит про диахронию, то употребляет слово «ряд», имея в виду последовательное расположение друг за другом языковых элементов;
2) когда речь заходит о том, что ближе к синхронии, то он пользуется словом «пучок», например, определяя фонему как пучок различительных признаков. В случае Фрейда слово «пучок» совершенно уместно, когда речь идёт о сгущении, что видно, например, в сновидении про монографию о ботанике, где в одной точке пересекается целый набор линий рассказа. Аналогично у Лакана, например, когда в Инстанции буквы… он говорит о синхронии в связи с означающим «дерево».
Отсюда можно задуматься об идее взаимодействия этих осей, ну, или инволюции между ними. Частично мы обнаруживаем это, когда, например, метонимию Якобсон определяет как проекцию того, что расположено на оси контекстуальной смежности (диахрония) на ось субституции (синхрония).
Так вот, в геометрии, говоря о полярности, мы имеем дело с переходом от того, что называют рядом точек, лежащих на одной прямой, к тому, что называют пучком прямых, пересекающихся в одной точке. Так мы и получаем первый перевод наших терминов между геометрическим и психоаналитическим дискурсами

рис. 6. Первая иллюстрация, в которой полярность предстаёт как инволюция между метафорой и метонимией.
Прежде чем сделать следующий шаг в геометрическом исследовании полярности, покажем простую иллюстрацию, которая опирается на перевод, указанный в предыдущем параграфе.
Пример мы позаимствуем из Мифологик Леви-Стросса, взяв примечательную трансформацию между двумя мифами о мёде. Эти мифы содержат любовные истории. В первом мифе любящим является мужчина, а во втором — женщина. Таким образом, они дуальны друг к другу. Однако Леви-Стросс обращает внимание, что когда женщина является любящей, то вместо одной мы имеем двух женщин — что-то избыточное для повествования. Загадка быстро находит решение, когда Леви-Стросс понимает, что мужчины любят не так, как женщины. Другими словами, существует два типа любви: мужская — буквальная, точнее метонимическая, и женская — метафорическая.
И, таким образом, переход между мифами является одновременно переходом от одной любви к другой, а след их различия приводит к удвоению женщин. Мёд в первом мифе фигурирует как метонимия сладкого, а во втором мифе (с метафорической любовью) он возникает как означающее, как имя объекта любви, то есть мужчины, которого зовут Мёд. Леви-Стросс отмечает, что любить этого мужчину — значит в переносном смысле любить мёд.
Другими словами, здесь мёд выступает как означающее желания, которое уместно обозначить лакановской матемой Ф. В другом мифе мёд, как мы и сказали, играет роль метонимии, что, в свою очередь, уместно обозначить матемой φ. Трансформация между
мифами, которая является переходом от отношений, где мужчина любит женщину, к обратным, где женщина любит мужчину, предстаёт как трансформация φ → Ф, ну, или как переход от метонимии к метафоре.
На самом деле, в мифе, где мёд играет роль φ, мы имеем два объекта любви, две точки, образующие ряд: мёд (пищевой) и женщина (половой). Любовь к ним идентична: она буквальна, можно сказать, лежит в регистре метонимии. В мифе, где мёд играет роль Ф и является именем желанного (причем не буквально, но в связи с означающим) мужчины, раздваивается уже не объект, но субъект любви, поэтому мы имеем двух любящих женщин.
Это и приводит нас к иллюстрации трансформации между этими мифами через полярность. Где S1, S2 — два мифа, трансформацию между которыми мы изучаем. Прямые обозначают субъектов любви, а точки — это объекты. В S2 мы видим две прямые (двух любящих женщин), которые пересекаются в одной точке (Мужчина по имени Мёд). В S1, наоборот, мы имеем две точки (Мёд и Женщину), через которые проходит одна прямая, отсылающая к заинтересованному в этих объектах мужчине. Как мы и сказали, переход от S1 к S2 предстаёт как переход между метонимией и метафорой.

рис. 7.
Наравне с этой иллюстрацией мы можем указать области психоаналитической теории, в которых такой полярный способ мыслить кажется совершенно оправданным:
1) дуальность между расщеплением субъекта и объекта, о которой Лакан говорит в работе Индивидуальный миф невротика. Напомним, что там речь идёт о том, что если мужчина достигает однозначности в социальной позиции, то он столкнётся с расщеплением любовного объекта, коррелирующим с тем, которое Фрейд описал, говоря про унижение любовной жизни. И наоборот, при однозначном определении любовного объекта мы обнаружим расщепление субъекта, которое Лакан иллюстрирует в том числе примером Гёте, которому для встречи с девушкой надо было переодеваться в бедняка;
2) полярность между перверсией и неврозом, на которых основывается композиция большей части 7 главы книги Вапперо Узел. Переход между этими структурами коррелирует с переходом между метонимией и метафорой, о чём Лакан пишет, например, в IV семинаре, думая, в частности, об отличии случая юной гомосексуалки (метонимия) от случая Доры (метафора);
3) переход между двумя типами женской гомосексуальности в работе Джонса.
Этот список можно продолжить, но, чтобы уточнить наш интерес к полярности, вернёмся на секунду к нашему простому примеру из Мифологик. Миф про мужчину по имени Мёд размещён Леви-Строссом в ряду мифов об ухудшении положения дел в мире индейцев. Этот миф имеет печальный конец, который состоит в том, что парень-Мёд был обрызган водой, взлетел вверх подобно пчеле и, оказавшись на вершине дерева, превратился в мёд совершенно буквальный. Вот так и вышло, что теперь мёд такой труднодоступный!
Но что значит эта последняя трансформация? Во-первых, мёд перестает работать как означающее Ф, отсылающее к сахарным устам, сладким объятьям, медовому месяцу и прочим любовным метафорам, и становится продуктом питания. Во-вторых, этот мёд располагается на вершине дерева, делается труднодоступным, превращается уже не просто из Ф в φ, но в -φ, ну, или в недоступный элемент, коррелирующий с нашими мнимыми точками на бесконечности. Ещё раз подчеркнём трансформацию этого мифа, резюмируя её следующим переходом:
Ф → -φ
Нам важно его подчеркнуть, чтобы не только иметь дело с инверсией, позволяющей записать полярность, но и вернуть наше внимание к недоступным элементам, отсюда возникает минус рядом с фи. Эта трансформация коррелирует с термином «разрыв кажимости», ну и, конечно, тоже имеет массу иллюстраций, одной из которых являются, наряду с этим мифом, голландские натюрморты в стиле vanitas, где часто полюс жизни вводится через метафору, например, горящей свечи, а полюс смерти возникает метонимически, через гниль или просто-напросто такой объект, как череп.

Это значит, что мы возвращаемся к вопросу о том, как полярность позволяет иметь дело с недоступными элементами. Исходя из него мы получим такую геометрическую версию трансформации, которая будет коррелировать с тем, что Лакан пытался вычитать, например, в анаморфозе, ну, или если ввести немного иной ракурс, то мы будем иметь геометрический способ говорить о метафоре, или переходе, обратном мифу про мёд, то есть о движении от -φ к Ф.
Геометрия метафоры
Итак, мы определили полярность и указали на некоторые области, где можно обнаружить её пользу для аналитического дискурса. При этом, кроме доступных и недоступных точек и прямых, у нас в руках оказался ещё один важный объект, а именно — коническое сечение.
Коническое сечение позволило построить полярность, поэтому само коническое сечение, или, как принято говорить в геометрии, ряд точек второго порядка (пучок прямых второго порядка) называют полярностью, ну, или её ядром. Интерес психоаналитиков к этому объекту может возникнуть не только потому, что Лакан рисовал случай Шребера, опираясь на гиперболу, но и в силу того, что конические сечения позволяют нам говорить о проблемах скопического влечения. Заметим, что когда окружность, эллипс, параболу и гиперболу называют коническими сечениями, то само слово «сечение» подразумевает, что эти четыре фигуры являются, по сути, четырьмя разными купюрами.
Так вот, говоря про видение, мы имеем в виду получение образа объекта. И это получение изображения объекта можно представить следующим образом:
1) мы имеем конус с вершиной в точке глаза, это подобно тому, как светит фонарик, только свет идёт не из него к объектам, а наоборот, от объектов в точку глаза;
2) потом мы сечём этот конус плоскостью, на которой, таким образом, и получаем изображение.

рис. 8. Если проявить осторожность в силу возможной путаницы между модальностями («звук», «свет») и лакановскими регистрами, то интересно сопоставить этот рисунок с тем, который Соссюр приводит в курсе общей лингвистики, когда речь заходит об определении означающего.
Если говорить в общих чертах, то деформация образа, которую мы имеем, например, в анаморфозе на картине Послы Гольбейна, опирается на то, под каким углом вы будете осуществлять сечение конуса. Короче говоря, в этой перспективе акт видения можно понять как купюру (сечение конуса видения), а анаморфоза особым образом связана с трансформацией между двумя разными коническими сечениями, ну, или между двумя разными разрезами. В лакановской записи это можно фиксировать как трансформацию S1→ S2, где S1 и S2 можно читать как две разные купюры (в нашем случае сечения), ну, или как два разных означающих, что для Лакана было почти идентичным (означающее ~ купюра).
При этом переход от одного конического сечения к другому можно рассмотреть не через смену угла сечения конуса плоскостью, но через инволюцию, то есть в нашем случае через полярность. Таким образом, мы переходим к обсуждению полярности (инволюции) между коническими сечениями, но напомним, что, как мы и сказали выше, полярность — это и есть коническое сечение.
Другими словами, мы будем говорить о том, что случается с коническим сечением при полярном преобразовании, то есть при применении к нему другого конического сечения.
Пусть дано коническое сечение S1 и другое коническое сечение, которое мы назовем $. Если применить полярность $ к точкам, лежащим на коническом сечении S1, то каждая из них превратится в прямую, которая будет касательной к ещё одному коническому сечению, которое мы назовём S2.
Схематично эта трансформация выглядит так:

рис. 9. Полярность $ ставит в соответствие точки конического сечения S1 касательным к коническому сечению S2.
Таким образом, мы можем сказать, что функция $ является инволюцией между коническими сечениями S1 и S2. Или, другими словами, композиция полярностей $ и S1 позволяет определить полярность S23.
Каков эффект этого перевода, ну, или этой замены S1 на S2?
Прежде чем его обсуждать, ещё раз подчеркнём принцип этой замены. Благодаря геометрии, да и в целом просто интуитивно, мы знаем, что одно коническое сечение преобразуется в другое проективно. К примеру, проекцией окружности может стать эллипс. Чтобы убедиться в этом, достаточно взять вырезанную из бумаги окружность и посмотреть на неё сначала сверху, а потом немного сбоку:

рис. 10.
Переход от взгляда сверху ко взгляду сбоку можно формализовать через понятие перспективы, ну, или перспективной трансформации. Эта трансформация, как мы видим, тоже переводит одно коническое сечение в другое. Однако она отличается от полярности прежде всего тем, что не является инволютивной функцией. Кроме того, и это будет для нас важно, такая трансформация переведёт центр одного конического сечения в центр другого, тогда как в полярности происходит, как мы сейчас попробуем показать, своего рода «децентрация».
В целом, для психоаналитических изысканий представляется интересным сопоставить эти два вида перехода между коническими сечениями. Первый (полярность) опирается на субституцию, на то, что Лакан называл символическим тождеством точек и прямых. Второй (перспектива) в данном контексте ближе к деформации образа, формы, зависит не от субституции, но от смещения центра проекции (положения глаза). Короче говоря, несмотря на то, что выглядят результаты этих трансформаций одинаково, пути, которые к ним ведут, различны. Сосредоточимся на эффектах первого из них (полярность).
Нарисуем две полярности, $ и S1, и их центры:

рис. 11.$, S1 — конические сечения. O$, OS1 — их центры.
Теперь мы будем брать элементы S1 и преобразовывать их посредством полярности $. Для примера возьмём произвольную точку A, лежащую на S1, и найдём её поляру a относительно $:

рис 12.Мы взяли точку А, лежащую на S1. Если бы мы строили её поляру относительно S1, то ей бы оказалась касательная к S1 в точке А. Однако мы строим её поляру относительно $ и получаем прямую а. Прямая а будет одной из касательных, очерчивающих коническое сечение S2, которое схематично мы показали на рис. 9.
Центром конического сечения мы будем называть точку, полярой которой это коническое сечение делает горизонт.
Давайте теперь узнаем, что сделает полярность $ с центром S1 и его полярой (линией на бесконечности):
1) начнём с поляры центра S1, то есть с горизонта. Из того, как мы определили полярность, очевидно, что полярность $ преобразует линию на бесконечности в свой центр, то есть в центр конического сечения $, который мы обозначили O$. Таким образом, мнимая линия на бесконечности станет действительной точкой;
2) теперь посмотрим, что станет с центром OS1. Если бы мы искали поляру этой точки относительно S1, то ей стала бы линия на бесконечности. Но теперь мы построим поляру центра S1 относительно другого конического сечения, то есть относительно $. В силу того, что центр S1 не совпадает с центром $, полярой OS1 будет уже не мнимая, а действительная линия.

рис. 13.
Таким образом, мы посредством $ перевели центр S1 и его поляру (горизонт) в два действительных элемента. Само S1 не могло этого совершить, потому что, хотя и делало горизонт действительным центром, одновременно превращало этот центр в недоступный горизонт, то есть просто меняло доступное и недоступное местами. Теперь мы имеем два доступных элемента: прямую a=$ (OS1) и точку A=O$=$ (горизонт). При этом А и а будут полярны относительно S2.
Это значит, что, оперируя действительными элементами полярности S2, мы можем делать выводы о том, что происходит с мнимой прямой S1. Например, если у вас есть какая-то задача на построение, где задействуется недоступная прямая S1, то можно перевести S1 в S2, потом решить задачу, пользуясь уже доступными прямой а и точкой А, после чего совершить обратный перевод. Другими словами, наш результат в том, что действительные элементы S2 получают переносный смысл, точнее, их можно читать буквально, как элементы S2, или в переносном смысле, как мнимые элементы S1. Замена S1 на S2 произвела метафору. Функцию, которую выполняет $, здесь можно мыслить либо как функцию перевода, либо как функцию чтения. В самом деле, как мы и говорили выше, с точки зрения проекции, ну, или с точки зрения перспективного преобразования S1 в определённом смысле ничем не отличается от S2: любое коническое сечение можно перспективно отобразить в любое другое коническое
сечение. При этом при проекции центр S1 перейдёт в центр S2, недоступная прямая останется недоступной прямой. С другой же стороны, получается, что функция $ позволяет произвести «децентрацию». В самом деле, посмотрим на вещи в контексте S2, которое мы будем читать уже не как проекцию S1, но как то, что получено из S1 через полярность. Теперь как центр и недоступную прямую S1 мы читаем точку (O$), не совпадающую с центром S2, и некоторую прямую (a), не совпадающую с горизонтом S2.
Ещё раз, учитывая, что вся наша история вертится вокруг производства недоступного элемента S1 как действительного, можно фиксировать наши преобразования через следующую формулу:

где а является продуктом трансформации.
В самом деле, получается, что мы на место одного конического сечения поставили другое коническое сечение, что привело к «означиванию» того, к чему первое коническое сечение отсылало, но что в его ситуации не было доступным. Как мы и сказали выше, эта геометрическая запись может быть переведена на «гуманитарный» язык благодаря истории про мёд, который из труднодоступного вещества (-φ) становится человеком, связанным с мёдом через означающее (Ф). Стоит при этом отметить, что инволюция точек и прямых в этой истории коррелирует с инволюцией между позицией субъекта и объекта (любящего и любимого) и, кроме того, схватывает удвоение субъекта и дуальное к нему удвоение объекта, которое в этой истории присутствует. Завершая эту часть, снова вспомним и про анаморфозу. По сути, мы получили геометрическую вариацию темы, которую она проблематизирует.

Анаморфоза является историей про пятно, которое играет роль -φ. Пятно недоступно не совсем как горизонт из геометрии, но с ним коррелирует по причине своей нечитабельности. При смене позиции зрителя, ну, или при определённом прочтении пространства пятно трансформируется в образ. В случае Послов Гольбейна речь идёт о пятне, которое превращается в череп.
При этом самое простое, что можно прочесть тут у Лакана, отсылает к нашей теме: происходит инволюция между позицией субъекта и объекта, потому как в определённый момент картина в некотором смысле обнаруживает, что знает, что на неё смотрят, ну, или в этом пятне на картине зритель вдруг узнаёт себя самого, обращённого из субъекта в объект а.
О влечениях и конических сечениях
В этой и следующей частях мы будем говорить о классификации конических сечений и об инволюции между ними. Другими словами, мы конкретизируем наш перевод S1 → S2, который до этого рассматривали безотносительно к типам конических сечений, которые в нём участвовали. Наша идея состоит в том, что инволюция между разными коническими сечениями может читаться в контексте лакановских трансформаций между разными топологическими поверхностями4,точнее, является вариацией этой темы. Другая близкая к нашей тема — это движение двух дырявых дисков, которыми Вапперо иллюстрировал как переход от отчуждения к сепарации, так и отличия между неврозом и психозом5.
Ещё раз скажем, что центром конического сечения мы будем называть точку, которую это коническое сечение переведёт в линию на бесконечности.
Тогда конические сечения можно классифицировать исходя из положения этого центра:
1) у эллипса центр внутри;
2) у гиперболы — снаружи;
3) центр параболы находится на ней самой и является точкой на бесконечности.
При этом в контексте проективной геометрии все эти конические сечения можно мыслить как разновидности эллипса.
Проиллюстрируем происходящее сначала на примере гиперболы, для этого нарисуем её в привычном виде:

рис. 14.
Асимптоты гиперболы являются касательными к ней в точках на бесконечности. Это значит, что горизонт будет полярой точки их пересечения. Другими словами, она и будет центром. При этом, по крайней мере, интуитивно, мы видим, что он (центр) находится снаружи гиперболы.
Рисунок позволяет понять, что ветви гиперболы дважды пересекают горизонт. Другими словами, учитывая наличие горизонта, мы можем мыслить гиперболу как эллипс, который пересекает линию на бесконечности:

рис 15. Гипербола как эллипс, который пересекает горизонт. Таким образом, гипербола содержит две точки на бесконечности, которые расположены там, где она касается своих асимптот.
Аналогично парабола является эллипсом, который касается линии горизонта, и эта точка касания и является его центром, потому как полярой к ней является сам горизонт:

рис 16. Парабола содержит одну точку на бесконечности, которая совпадает с её центром.
Таким образом, мы получаем три положения конического сечения относительно горизонта и относительно собственного центра:

рис. 17.
Если бы горизонт был действительной линией, то переход между коническими сечениями можно было бы представить как привычное (евклидово) движение конического сечения, которое сначала её касается, а потом пересекает. Но горизонт не является действительной линией, ну, или, точнее говоря, движение, которое мы определяем в евклидовой геометрии, как раз так и определено, что до горизонта «доехать» не получится. Для наглядности можно представить поезд, который едет по рельсам в сторону горизонта, но, как бы долго он не ехал, он не сможет его коснуться. Таким образом, евклидовы движения не могут привести к трансформации одного конического сечения в другое, потому как эта трансформация подразумевает то, что несколько неформально можно назвать способностью пересекать горизонт.
Что касается перевода этой невозможной для евклидовых движений трансформации в область психоанализа, то нам кажутся перспективными не только те контексты, которые мы указали выше, но и то, что с ними связано, а именно — трансформация объекта влечения.
Прежде всего, практика показывает, что влечения не всегда ходят по одиночке, и в одном и том же случае вы обнаружите, например, наложения аудиального и орального с анальным, ну, и т. п. Причём в этом пункте Лакан скорее придерживается такого почти геометрического подхода, в семинаре Объект психоанализа он говорит: “Ни один элемент не сможет выполнять функцию объекта а, если он не будет связан с другими объектами в том, что называют структурой группы”. В этом же семинаре он предлагает классификацию объектов влечений, которая устроена как группа Клейна. Для её построения он применяет дихотомию «желание/требование», составные части которой могут быть адресованы Другому или ему принадлежать. Другими словами, речь идёт о 4 элементах:
1) оральный: требование у Другого (demande à l’Autre);
2) анальный: требование Другого (demande de l’Autre);
3) скопический: желание к Другому (désir à l’Autre);
4) аудиальный: желание Другого (désir de l’Autre).
Одним словом, и в геометрии, начиная с программы Ф. Клейна6, и в антропологии, начиная с Леви-Стросса7, и в психоанализе объект предстаёт через его трансформацию8.
В конце концов, после чтения Фрейда можно понять, что главным в структуре влечения является его судьба.
Конические сечения в этом контексте как раз и интересны своей трансформацией. При этом хочется не только указать путь трансформации одного конического сечения в другое, что мы сделаем ниже, но и подумать о том, как интерпретировать их различия.
Прежде всего, можно заметить, что в представленном нами способе изображать эти объекты имеют место элементарные различия, которые легко прочесть на наших рисунках. Видно, что гипербола является такой своего рода вывернутой окружностью (эллипсом). Центр гиперболы находится снаружи, тогда как сама она пересекает его поляру (горизонт), и наоборот: центр эллипса находится внутри, тогда как его поляра (горизонт) находится снаружи. Парабола, соответственно, выступает промежуточным пунктом между этими двумя состояниями: её центр находится ни внутри, ни снаружи, но на границе между ними.
Означающее «центр» может оказаться полезным для того или иного варианта перевода этого материала на психоаналитический прежде всего потому, что обыденное значение слова центр отсылает к чему-то, что трудно представить снаружи того, центром чего он является. Однако в таком разрезе психоаналитики и подходят обычно к объекту малое а, который мыслят как «обладающий способностью» совмещать интимное и чуждое.
Например, можно вспомнить, что про эту дихотомию часто говорят, описывая феномены психоза. Известно, что вербальные галлюцинации связаны с непризнанием собственного голоса, то есть ты слышишь речь, которую больше не считаешь своей. Другими словами, воспринимаешь нечто внутреннее как внешнее. Таким образом, мы имеем две крайние позиции, коррелирующие с переходом от окружности к гиперболе:
1) свой голос, который узнаёшь;
2) свой голос, который не узнаёшь, то есть воспринимаешь как что-то внешнее и чуждое.
Ну, и промежуточный пункт между ними мы имеем, сталкиваясь с феноменами психического автоматизма, описанными Клерамбо. Например, речь идёт о том, что называют эхом мыслей. Эхо мыслей — это тот момент, когда ты понимаешь, что это твои собственные мысли, но они будто приходят к тебе извне. Таким образом, психоз совершает траекторию, обратную той, которую Фрейд сделал принципом психоанализа. Wo Es war, soll Ich werden подразумевает, что Я являюсь там, где было Оно, то есть Я должен узнать себя там, где было нечто другое и чуждое, тогда как в психозе, наоборот, нечто иное обнаруживается там, где было Я, и инаковость этого интимного только усиливается9.
Эту иллюстрацию стоит воспринимать как набросок перевода геометрической трансформации в нашу пси-область, и, конечно, таких более или менее точных интерпретаций может быть несколько, более того, этот плюрализм интерпретаций в некотором смысле является желательным, так как позволяет уйти от словарного соответствия между геометрическим и психоаналитическим материалом, то есть уйти от фиксированного кода к лучшему (в идеале) пониманию структуры происходящего. С другой стороны, кажется ясным, что понимание структуры по идее ограничит многообразие интерпретаций, ну, или сделает их точнее.
На данный момент мы воспользовались идеей разного положения центра конического сечения (внутри/снаружи/на границе), что коррелирует с разным положением самого конического сечения относительно горизонта, то есть относительно поляры этого центра. Другими словами, мы получили отличия, которые позволяют достаточно ясно сформулировать, чем, например, гипербола отличается от эллипса, что до этой презентации не было таким очевидным. Параллельно мы заметили, что существенной характеристикой объектов влечения является вопрос интимности/чуждости, ну, или вопрос об их принадлежности субъекту или Другому: так, например, грудь Лакан мыслит как часть субъекта, «налепленную» на Другого, экскременты он мыслит тоже исходя из двусмысленности того, кому они принадлежат (часть себя, которую надо этому другому отдать), etc. Отсюда мы и имеем историю с разными положениями центра, который читается как объект.
Одновременно, как мы уже в целом заметили выше, когда мы имеем горизонт, линию на бесконечности, предстающую в модели проективной плоскости разрезом на ленте Мёбиуса, то мы сталкиваемся с купюрой, которая отсылает уже не к объекту, а к субъекту. Тогда мы можем вернуться к дихотомии «объект/субъект» и переход от эллипса к гиперболе мыслить в связи с матемой фантазма ($<>a), которая в данном контексте предстаёт как пульсация между недоступным (для эллипса) горизонтом и, наоборот, недоступным, ну, или внешним (для гиперболы), центром.
Пересекая горизонт
Вернёмся к вопросу инволюции между коническими сечениями. Наш тезис состоит в том, что инволюцию между коническими сечениями можно формализовать, если учесть отношения, в которых находятся переводимое и то, что осуществляет функцию перевода. В предыдущей части мы не учитывали, каким образом окружность S1 расположена по отношению к окружности $, ну, или, что более существенно, в каких отношениях S1 находится с центром $.
Для наглядности рассмотрим пример. Пусть S1 касается центра $.

рис. 18.Условия перевода.
В этом случае получится, что $ переведёт точку S1 (ту в которой S1 касается центра $) в линию на бесконечности. Эта линия на бесконечности будет касательной к S2 и, соответственно, она коснётся S2 в недоступной точке. Таким образом, у S2 будет один недоступный самосопряжённый элемент: точка на бесконечности, которой в полярности S2 будет соответствовать линия на бесконечности.
Схематично S2 можно изобразить так:

рис. 19. Результат перевода.
Другими словами, S2 будет представлять собой параболу (см. рис. 16-17). Итак, оказалось, что наш пример — это пример инволюции между окружностью и параболой. Ещё раз подчеркнём, что переход от окружности к параболе мы осуществляем не путём перспективного преобразования, но с помощью полярности, которая меняет точки на прямые, то есть инволютивно.
Теперь пусть центр $ лежит снаружи S1:

рис. 20. Ещё одни условия перевода.
Тогда найдутся такие два диаметра $, которые будут касательными к S1:

рис. 21.
$ переведёт:
1) диаметр a в точку на бесконечности А;
2) диаметр b в точку на бесконечности B;
3) точку касания N в прямую n, на которой будет лежать точка А;
4) точку касания M переведёт в прямую m, которой будет принадлежать точка B.
В силу того, что а и N, а также b и M были самосопряжёнными элементами полярности S1, они перейдут в самосопряжённые элементы полярности S2. Другими словами, прямая n будет касаться S2 в недоступной точке А, а прямая m будет касаться S2 в недоступной точке B.
Схематично можно изобразить S2 следующим образом:

рис. 22. Результат перевода.
Другими словами, S2 будет представлять собой гиперболу, асимптотами которой будут m и n. Итак, перед нами инволюция между окружностью и гиперболой.
Путём аналогичных размышлений можно получить ответы и для всех остальных случаев перевода. При этом оказывается, что на результат перевода влияет не то, каким коническим сечением является S1 (оно может быть любым), но то, в каких оно отношениях с центром того, что его переводит, то есть с центром $.
В итоге мы получаем простой способ сказать, какой результат вы получите при переводе.
Для этого достаточно взглянуть, как расположены S1 и центр $:
1) если центр $ будет снаружи S1, то S2 будет гиперболой;
2) если центр $ будет касаться S1, то S2 будет параболой;
3) если же центр $ будет внутри S1, то S2 будет окружностью.
Получается интересный принцип: точки одного конического сечения (S1) и центр другого (центр $) являются изображением третьего конического сечения (S2), то есть того, которое получается при переводе первого вторым10.
Теперь первое коническое сечение можно изображать только окружностью, а второе коническое сечение можно изображать только его центром, так как это единственная существенная характеристика для перевода:

рис. 23. Чёрная точка — центр $, окружность — S1.
Чтобы сформулировать общий для всех трёх случаев принцип, посмотрим на ситуацию, когда центр $ снаружи S1. В этом случае S2 будет гиперболой, но гипербола и есть фигура, центр которой находится снаружи. Таким образом, ещё раз подчеркнём, что рисунок, который изображает взаимное положение переводимого и переводящего, одновременно позволяет прочесть результат перевода. Аналогично во всех трёх случаях.
Теперь перейдем к вопросу, о котором мы говорили в начале. Звучит он несколько странно, примерно так: существует ли способ как-то связать друг с другом евклидово движение и пересечение горизонта, учитывая, что евклидово движение по определению не может его пересечь?
Как мы видим, центр $ совершает вполне классическое (евклидово) движение по отношению к S1: движется снаружи внутрь, ну, или если читать в обратном порядке, то изнутри наружу. Одновременно это движение производит модификацию результатов нашего перевода, то есть модификацию конического сечения S2=$(S1). Получается, что при евклидовом движении центра $, S2 оказывается в разных положениях относительно горизонта:

рис. 24. Пересекая горизонт.
Инволюция (полярность) не является тем, что отрицает недоступное, но тем, что позволяет им оперировать, подобно тому как острота не упраздняет измерение «между строк», она не превращает несказанное в сказанное буквальным способом, но тем не менее эффективно с этим несказанным обходится. У нас и получилось, что инволюция между S1 и S2 позволяет читать движение S1 относительно точки (центра $) как перемещение S2 относительно прямой (горизонта). Другими словами, когда с S1 происходит вполне евклидово преобразование (движение), то одновременно с тем объектом, который, пользуясь выражением Лакана, является этому S1 тождественным и различным (с S2), происходит трансформация, которая в евклидовой геометрии не пишется, потому как S2 модифицируется от эллипса к гиперболе, ну, или, образно выражаясь, пересекает горизонт.
Скажем так, контекстуальные перемены S1 инволютивно тождественны структурным переменам S2. Это значит, что наши построения в том числе подводят нас к геометрической интерпретации канонической формулы Леви-Стросса11, в которой инволюция между термином и функцией сопровождается прибавочным различием, которое возникает на уровне одного из членов этой пары: термин а переходит в а-1. Основная идея, которую внёс Леви- Стросс своей формулой, состоит в том, что при вполне симметричных переменах между двумя объектами (например, между мифами) мы обнаружим дополнительный переворот, который
вносит в симметричные различия некую асимметрию. Например, речь идёт про переход от метонимии к метафоре, как в примере из мифов про мёд, которые на первом этапе различались совершенно симметрично: в одном мужчина любит женщину, а в другом — наоборот.
В нашем случае речь тоже идёт о вполне симметричной дуальности точек и прямых, которая ставит в соответствие коническому сечению S1 другое коническое сечение S2, ну, или трансформирует первое во второе. Однако эта трансформация не проходит бесследно, потому что евклидово движение S1, ну, или нечто, что можно прочитывать как перемены c ним на диахроническом уровне, возникает на уровне S2 уже не просто как движение «в обратную сторону», но как преобразование, которое, строго говоря, евклидовым движением не является.
Когда Леви-Стросс говорил про связь своей формулы мифической трансформации с математикой, то подчёркивал, что мифическую трансформацию не получится «засунуть» в одну единственную группу в силу того, что её принципиальным пунктом является то, что он называл драматическим скачком. Драматический скачок подразумевает не только трансформации внутри какой-то группы, но её размыкание, выход в другую группу, иными словами, использование того, что в первой группе не пишется. Вот пункт, где у него возникает регистр Реального. Он сравнивал это с переключением скоростей на велосипеде: когда цикл готов завершиться, то цепочка переключается на другую «звезду»… Другими словами, вариация между двумя мифами подразумевает трансформации и инверсии терминов, но с одновременной сменой структуры, про которую мы иногда говорим как про что-то вроде вторжения асимметрии в симметрию.
Однако теперь наша формулировка становится точной и резюмируется в двух пунктах:
1) мы говорим, что движение одного конического сечения относительно точки инволютивно трансформируется в движение другого конического сечения относительно прямой. Это уровень «симметрии». И здесь мы находимся в группе евклидовых преобразований (в нашем случае движения);
2) евклидово движение первого конического сечения провоцирует «пересечение горизонта» вторым коническим сечением. Вот вторжение «асимметрии». Так как здесь то, что инволютивно тождественно евклидовым движениям, становится одновременно от них отличным, не пишется в них, так как происходит в другой структуре, а именно — в группе проективных преобразований. Тем самым группа размыкается, и мы получаем геометрическую версию леви-строссовской трансформации, которая одновременно является геометрической версией лакановской инволюции означающего.
Итак, на этом мы завершили классификацию инволюций между коническими сечениями12.
Несколько слов о кросс-кэпе
Всё, что мы изучали в предыдущих частях, происходило на проективной плоскости.
Моделью проективной плоскости является кросс-кэп13.
Переход от эллипса к гиперболе можно получить путём перемещения окружности по поверхности кросс-кэпа таким образом, чтобы она превратилась в известную лаканистам внутреннюю восьмёрку. Реализацию такого движения наглядно показывал Ж.-М. Вапперо.
Мы же ограничимся здесь тем, что укажем, почему одним из вариантов изображения гиперболы на кросс-кэпе является внутренняя восьмёрка, а также некоторыми соображениями о связи полярности и двух разрезов на этой поверхности, которые интересовали Лакана.
Чтобы увидеть гиперболу на кросс-кэпе, удобно воспользоваться его частью, а именно — лентой Мёбиуса. Сначала возьмём прямоугольник, нанесём на него изображение гиперболы14 и закрутим в нашу одностороннюю ленту:

рис. 25. Один из способов представить гиперболу на ленте Мёбиуса15.
Мы видим, что гипербола, попав на ленту, стала выглядеть как внутренняя восьмёрка, — так, она и будет выглядеть на кросс-кэпе.
Тогда на нём переход от эллипса к гиперболе можно резюмировать следующим образом:

рис. 26. Движение S1 → S2 будет выглядеть как трансформация диска во внутреннюю восьмёрку и может читаться как переход от эллипса к гиперболе16. На рисунке видно, что в случае S1 (эллипса) очерчивается диск, а в случае S2 (гиперболы) гораздо более явным становится очерчивание вложенной на поверхность кросс-кэпа ленты Мёбиуса.
Покажем на нашем рисунке, во что стягивается S1 и во что стягивается S2:

рис. 27. Точкой и матемой а (объект а) мы обозначили то, к чему стянется S1, если уменьшать его размер. S2 стянется к линии (матема $, отсылающая к субъекту), которая выглядит как окружность, однако мы подписали её словом «прямая», потому как данная окружность на кросс-кэпе является моделью проективной прямой17.
О чём нам говорит рисунок 27? Прежде всего, стоит напомнить, что если выколоть из кросс-кэпа точку, то он превратится в ленту Мёбиуса, а если убрать из него прямую (то, что мы обозначили прямой в состоянии S2), то он станет двусторонним диском. Собственно, так и устроены две купюры, которые Лакан исследовал на кросс-кэпе, и теперь мы видим, что они полярны:
1) купюра No1. Точка = полюс = объект малое а;
2) купюра No2. Прямая = поляра = разрез на ленте Мёбиуса = субъект $.
Таким образом, мы получаем связь отношений между односторонней и двусторонней поверхностью и полярностью точек и прямых. Когда Лакан рисовал на кросс-кэпе две купюры, которые дают то диск, то ленту Мёбиуса, что же он делал? Теперь мы понимаем, что он, по сути, был занят разновидностью инволюции, которую называют полярностью.
Полярность — это понятие, которое лежит в основе пульсации не только между точкой и прямой, но и между двусторонним и односторонним. Такая связь напрямую связана с тем, что моделью проективной плоскости является односторонняя поверхность. Инволюция является не просто понятием, которое Вапперо взял из проективной геометрии и использовал там, где Лакан говорил о том, как одностороннее переходит в двустороннее. Теперь мы понимаем, что на самом деле полярность (инволюция) является основанием этого перехода.
Завершение
Вклад Ж.-М. Вапперо в психоанализ, на наш взгляд, состоит прежде всего в его подходе к письму. Он не просто является автором, который пишет учебник, в котором пытается объяснить, как Лакан использовал топологические объекты. Его принцип чтения кажется гораздо более перспективным: он подталкивает к использованию топологического материала, его доработке, перезаписи. Вапперо не объясняет топологию Лакана — он её практикует.
В итоге, он, если так можно выразиться, инволютивно трансформирует написанное Лаканом, производит модификацию. И, как уже, наверное, стало ясно из нашего текста, модификация объекта — это, в конце концов, и есть эффективный способ его понять и сохранить.
Наш текст, безусловно, вдохновлён позицией, которую Вапперо адаптировал к текстам Лакана. При этом мы попробовали обратиться к той области, которая не была заявлена в его топологии эксплицитно. Лакан говорил про графы, поверхности и узлы, однако в этом списке нет конических сечений, поэтому, например, в тетрадях результатов Вапперо нет отдельного
выпуска, посвящённого им.
Этим текстом мы хотели восполнить эту нехватку и, кажется, смогли убедительно показать, что выбор теории конических сечений не является случайным. Коническое сечение — объект, который в проективной геометрии называют полярностью. Полярность — разновидность инволюции, которая, среди прочих её достоинств, является тем, что и лежит в основе лакановских исследований перехода между односторонними и двухсторонними поверхностями. Одним словом, если мы действительно считаем инволюцию означающего инвариантом лакановского учения, то обращение к коническим сечениям является совершенно естественным просто потому, что они являются её вторым именем.
- Тут уместно сослаться на доклад Н. Шароповой на конференции TEE Знание теории, которого она не знает. В нём она наглядно показывает, что мнимая прямая может быть рассмотрена как инвариант евклидовой геометрии. Другими словами, движения евклидовой геометрии оставляют её неподвижной, никак не меняют. Согласно же, например, Ф. Кляйну, объект той или иной геометрии как раз и определяется через то, что является инвариантным относительно её преобразований. Например, обычный взгляд на евклидову геометрию говорит нам, что её трансформации не меняют расстояния между точками: можно вращать или отражать треугольник, но с точки зрения расстояний между его вершинами он останется «собой». Так вот, Шаропова подчёркивает, что мы можем иметь альтернативный взгляд на объект евклидовой геометрии: она оставляет неподвижным горизонт, а значит он и выступает как её объект, несмотря на своё отсутствие, то есть несмотря на то, что он в евклидовой геометрии никак явным образом не фигурирует. ↩︎
- Чтобы сделать более доступным интуитивное понимание психоаналитического контекста нашей работы, напомним о сновидении, которое Лакан использует, чтобы говорить о регистре Реального. Речь о сновидении о горящем ребёнке из 7 главы работы Фрейда Толкование сновидений. Завораживающим моментом истории этого сновидения является тождество того, что происходит во сне, где отцу является его ребёнок и сообщает ему, что он горит, и того, что происходит в реальности, где труп ребёнка действительно загорелся. Другими словами, мы имеем тождество двух, казалось бы, различных пространств: сна и бодрствования. Отсюда мы уже можем составить интуитивное понимание инволюции, которую Лакан определял как пару, которая объединяет идентичное с различным, ну, или просто через тождество различного. Кроме того, пример этого тождества возникает ровно в той точке, которую Лакан обозначал как встречу с Реальным. ↩︎
- Можно доказать лемму:
композиция двух полярностей определяет третью полярность.
Доказательство
Пусть дана точка А и её поляра а относительно S1.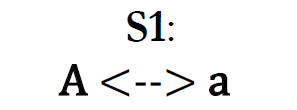
Точку, которой полярность $ поставит в соответствие прямой а, назовём А’, прямую, которую полярность $ поставит в соответствие точке A, назовём а’: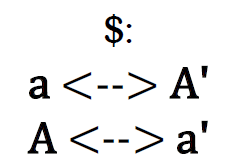
Таким образом, композиция этих функций $(S1) однозначно поставит в соответствие точке А точку A’, прямой а — прямую а’:
Тогда мы получаем полярность S2, которая будет ставить в соответствие точке А’ прямую а’: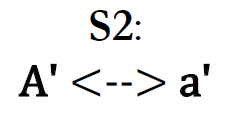 ↩︎
↩︎ - Речь идёт, например, о переходе от тора к ленте Мёбиуса. ↩︎
- По сути, это движение, которое можно читать как движение структуры, сводилось к взаимодействию двух нехваток: дыры в диске $ и дыры в диске A. ↩︎
- Собственно, именно благодаря Ф. Клейну в геометрии математики стали определять объект через группу трансформаций. ↩︎
- Как уже было сказано, для Леви-Стросса миф является его трансформацией. ↩︎
- В этом контексте можно ещё вспомнить, например, человека с крысами. Ход лечения этого пациента обнаруживает последовательную трансформацию крыс, которые сначала представали через пытку как то, что попадает внутрь тела. Потом сам этот человек вспоминал, что любил кусать, как крыса. В итоге крысы превратились в детей, а сама пытка стала вариацией инфантильной анальной теории рождения, то есть историей о том, как что-то уже не заходит внутрь, а наоборот — перемещается наружу. ↩︎
- См. на эту тему, например, E. Porge. Les voix, la voix, Essaim 2011/1 (n° 26). ↩︎
- Сначала на картеле мы составляли полную табличку переводов, пока Ольга Бронникова не заметила этого принципа. ↩︎
- Речь идёт о его знаменитой формуле, которая попала к психоаналитикам благодаря Лакану: Fx(a): Fy(b) :: Fx(b): Fa-1(y). Прибавочную трансформацию а→ а-1 Лакан связывал с регистром Реального. ↩︎
- Случай, который мы не приняли в расчёт, состоит в ситуации, когда центр $ совпадает с центром S1. Можно было бы сравнить этот случай с промахом чтения, который состоит в том, что линия на бесконечности остаётся линией на бесконечности. Другими словами, промах приводит к тому, что мы не можем рассматривать некоторую действительную прямую в переносном смысле, как делали это в части текста Геометрия метафоры. ↩︎
- В этой части мы не будем подробно разбирать структуру и свойства этой поверхности. Наша цель здесь лишь в том, чтобы ещё раз обосновать уместность понятия полярности, и в некотором смысле эта часть является избыточной для общего хода изложения. С другой стороны, мы решили её оставить, потому как здесь намечаются мосты между коническими сечениями и лакановским подходом к поверхностям, а также появляются некоторые вопросы, которые могут стать началом дополнительных исследований. ↩︎
- Читателю предлагается подумать о том, каким образом на ленте Мёбиуса будет представлена парабола. ↩︎
- Нетрудно догадаться, что можно получить и второй. Для этого достаточно ветви гиперболы расположить в других зонах, очерченных асимптотами. В этом случае она будет выглядеть как эллипс. Отсюда можно было бы задаться некоторыми, может и незначительными, хотя и интересными для понимания происходящего вопросами, но здесь мы этого делать уже не будем. ↩︎
- Как мы уже сказали, подробнее это перемещение диска по кросс-кэпу можно посмотреть в работах Ж.-М. Вапперо. ↩︎
- Оставляем без объяснения тот факт, что моделью проективной прямой является окружность, в надежде, что все уже знают это либо из геометрии, либо из работ Лакана и Вапперо. Эта часть работы, как мы и говорили, носит скорее дополнительный характер и является не слишком заботливой о читателе, так как подразумевает либо наличие некоторых знаний, либо подталкивает к их приобретению. ↩︎