---

Текст:

Содержание

Введение

Аристотель и Лао Цзы

Лао Цзы и Кантор

Кантор и Маркс

Маркс и Лакан

Психоанализ и Топология

Введение

Современная критика часто обвиняет психоанализ в консервативности. Например, психоаналитики упрямо используют бинарное отличие мужчина\женщина, в мире, где небинарность для многих уже стала более менее естественным способом мыслить. В этой критике психоанализ предстает как теория, которая заражена патриархальным взглядом, где его догмы, вроде зависти к пенису у женщин, выглядят как что-то, продиктованное самим порядком вещей. Порядком, который никогда не ставится под сомнение, но на деле оказывается культурно обусловленной особенностью, а вовсе не структурной необходимостью. Психоаналитики в этом свете предстают как чудаки, продвигающие ситуативные истины прошлого, как истины вечные. Будто бы они подобно Дону Кихоту, который продолжал верить в рыцарей в эпоху, когда их не существует, верят в вещи, вроде Эдипова комплекса, запрета на сексуальность и т.п. в мире, который давно уже находится совсем в другой точке своего развития. 

Может ли психоанализ выпутаться из этой критики? Нам кажется, что это вполне возможно, если сконцентрироваться на том, каким образом в психоаналитическом дискурсе осмысляют и используют саму идею различия. Тогда мы окажемся в мире логики. В ней, конечно, можно двигаться путем “небинарности”, вроде логик, где кроме истины и лжи существуют промежуточные значения. Однако среди современных подходов к логике, “небинарность” противостоит “бинарности” не так как современное чему-то прошлому и устаревшему. Развитие логики не обязательно является движением в сторону такого, если так можно выразиться, линейного увеличения числа различий, но может происходить в сторону осмысления самого понятия различия, и именно в этой области как нам видится располагает себя и психоанализ.

Этот текст является первой частью из двух работ, посвященных различиям. В том числе его можно рассматривать как введение в теорию множеств для гуманитариев, так как его основные построения опираются на азы этой системы письменности. Введение в данном случае не означает, что мы просто рассказываем, что вот, мол, есть такая теория, и вот как в ней всё устроено. Идея в том, чтобы показать, каким образом вводными данными теории множеств можно пользоваться в контексте другого дискурса, то есть пользоваться ими вне математики. Таким образом, это проект скорее в стиле Лакана и Вапперо, которые пытались заимствовать письменность из одного дискурса для использования в другом дискурсе, по аналогии с тем, как японская письменность заимствует иероглифы из китайского языка. Нужды этого другого дискурса в данном случае связаны с двумя текстами, ну или, лучше сказать, с двумя концептами. Первым является прибавочная стоимость Маркса, а вторым определение желания из работы Лакана “Значение фаллоса”. Оба, как мы покажем, могут быть записаны при условии, что мы учтём новости, которые появляются в подходе к различиям, когда от логики Аристотеля мы переходим к теории множеств Кантора. 

Ещё одним важным именем собственным для нашего текста о различиях будет Лао Цзы, на чьей цитате мы закончим это введение:

“Тридцать спиц соединяются в одной ступице, [образуя колесо], но употребление колеса зависит от пустоты между [спицами]. Из глины делают сосуды, но употребление сосудов зависит от пустоты в них. Пробивают двери и окна, чтобы сделать дом, но пользование домом зависит от пустоты в нем. Вот почему полезность чего-либо имеющегося зависит от пустоты”.

Аристотель и Лао Цзы

Логика в этом тексте будет выступать для нас не только как знание о том, как мыслить правильно, но и как теория, которая определенным образом вводит нас в мир различий, в разные миры различий. 

Когда мы говорим о логике Аристотеля, то мы сразу попадаем в мир классификации: род и вид являются определенным способом внести различия. Подход Аристотеля мы резюмируем диаграммами, которыми иллюстрируют аксиомы силлогизмов и которые по сути обращаются к дихотомии, которую мы будем называть: внутри\снаружи. Вот, эти диаграммы: 

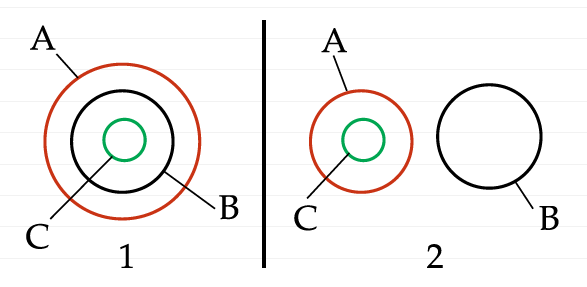
Как мы видим, обе аксиомы касаются отношений между тремя окружностями. Одна окружность может быть либо внутри другой, либо снаружи. В первой аксиоме нам говорят, что если окружность B лежит внутри окружности A, и окружность С лежит внутри окружности B, то окружность С лежит внутри окружности А. Этот рисунок можно проиллюстрировать знаменитым силлогизмом про Сократа: “Все люди смертны. Сократ человек. Значит, Сократ смертен”. Графический перевод этого силлогизма как раз и состоит в том, что кружок “люди” находится внутри кружка “смертные”, тогда как кружок “Сократ” находится внутри кружка “люди”, а значит кружок “Сократ” находится внутри кружка “смертные”, Аналогично устроена вторая аксиома. Если А снаружи B, а С внутри А, то С снаружи B. 

Вторая аксиома для нас будет примечательной как раз в силу того, что позволяет отличить логику Аристотеля от подхода, который мы можем найти у Лао Цзы. Для этого немного модифицируем ее рисунок, вводя дихотомию между цветами. Пусть чёрное — это не белое. Тогда чёрное на диаграмме отображаем снаружи белого. 

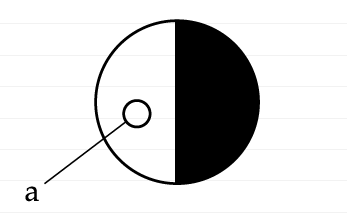
Из диаграммы этой аксиомы понятно, что если что-то находится в зоне слева (окружность обозначенная буквой а), то есть, снаружи правой зоны, то это что-то невозможно рассматривать как относящееся к этой правой зоне. Другими словами, диаграмма Инь/Янь является с точки зрения аристотелевской логики противоречием. Внутри Янь не может быть того, что относится к Инь, так как Инь это то, что было введено через внешнюю к Янь зону. Таким образом, мир различий Лао Цзы отличается от мира Аристотеля, нарушает аксиомы силлогизмов.

Одним из ярких и достаточно понятных примеров реализации на практике этих различий является китайская живопись, которую, согласно Франсуа Чангу, можно понимать как способ наглядно представить эту логику. Так, например, в качестве первоначального различия может выступить небо и земля или пустое и полное. Однако, рисуя что-то полное, относящееся к миру земли, в это полное вносят пустое. К примеру, пустотой нарисован камень на следующей картинке:

Как мы видим, там, где нужно было бы рисовать «материю» камня, то, что находится внутри и относится к земле, появляется небо, пустота. Камень таким образом нарисован скорее не как вещь, но благодаря тому, что задействуется промежуточное пространство между ним и другими вещами. Оно заполняется, а камень оставляют пустым. Хотя обычно мы думаем наизнанку, относя вещи к чему-то полному, а промежуток между ними считая пробелом. 

Таким образом, возможность рисовать землю небом и полное пустым подразумевает, что логика отношений содержимого и содержащего должна получить какую-то  модификацию.

Лао Цзы и Кантор

В западной мысли такой модификацией логики Аристотеля является теория множеств Кантора. Потрясающие возможности этой новой логики или этой системы письма начали проникать в психоанализ благодаря сначала Лакану, а потом Вапперо. 

Но что конкретно меняет переход от аристотелевских классов к канторовским множествам? 

Благодаря Кантору, логика делает большой шаг вперед по той причине, что наряду с внутри\снаружи появляется новое различие¹, ну или можно сказать, что в подходе к различиям появляется новый объект. Допустим мы имеем класс как набор неких объектов, но в теории множеств начинаем рассматривать и сам этот класс как объект. Другими словами, если классификация Аристотеля занималась тем, что отличала то, что находится по одну сторону от границ от того, что находится по другую сторону, то в теории множеств мы начинаем рассматривать и сами границы. В некотором смысле это значит, что помимо того, что мы различали вещи мы получаем возможность различать различия между этими вещами.

Эффекты этой модификации можно посмотреть на диаграммах, которые снова, как и в случае с Аристотелем, мы нарисуем концентрическими окружностями.

Как их рисовать? Во-первых, теория множеств — это теория отношений, которые обозначают знаком “∊”, и обычно читают как принадлежность. Как нарисовать, отношения A ∊ B, ну или А принадлежит B? Оба множества обозначим окружностями, и окружность А разместим внутри окружности B. 

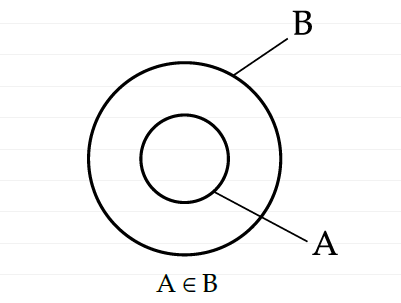
Теперь, пусть есть С, которое принадлежит А: C∈ A. Тогда, С мы нарисуем внутри окружности А. Вот, как выглядят теперь наши два условия, которые совпадают с условиями для приведенной выше аристотелевской аксиомы силлогизма: 

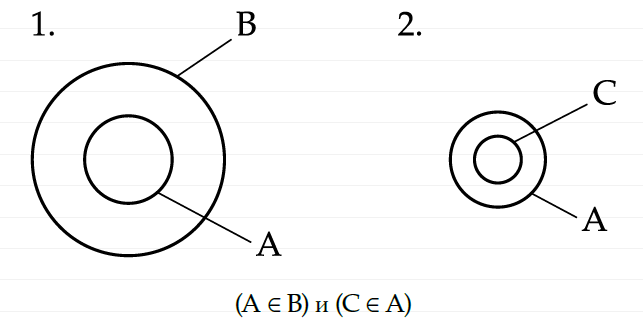
Итак, множество С находится внутри множества А, а множество А находится внутри множества B. Отсюда, казалось бы, следует, что множество С должно находиться внутри множества B, ведь С является содержимым А, а само А содержится в B. Но теперь, во вселенной Кантора, это не так, точнее, это не обязательно так!

Другими словами, отношения принадлежности так устроены, что если содержащее где-то находится, то это не значит, что содержимое этого содержащего находится там же. Это подобно китайскому пейзажу, который мы обсудили выше: земля (содержащее) находится снизу (снаружи) неба, но содержимое земли (камень) нарисован пустотой (небом), то есть “располагается” не там, где земля, которая его содержит.

Говоря чуть более формально: в отношениях принадлежности транзитивность не обязательно выполняется. Приведем пример не из живописи, но из мира множеств: если вы в качестве А возьмете множество всех конечных множеств, тогда любое его содержимое (С) будет конечным. При этом само А будет бесконечным, потому что разных конечных множеств бесконечно много, то есть А будет лежать внутри множества бесконечных множеств (B), а его содержимое (С) должно находиться снаружи B, потому что является конечным. 

Дополним нашу картинку этой ситуацией: 

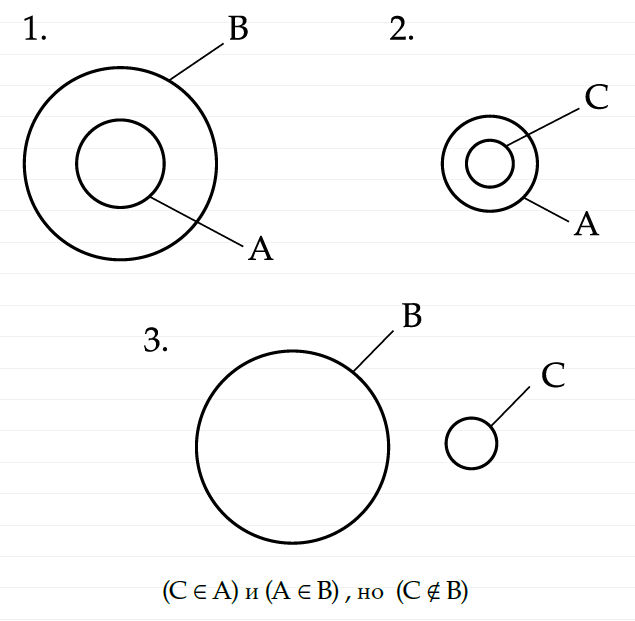
В частности эта ситуация показывает, что воображать множества в виде сумок, как это подсказывает интуиция и как этому часто учат в школе, не всегда является самым точным способом. Сумки устроены транзитивно. Вы например, идете за покупками с сумкой. Потом берете помидоры, кладете их сначала в целлофановый пакет, а потом в вашу сумку. Помидоры, находятся внутри пакета, а он внутри сумки, но и помидоры тоже находятся внутри нее. В теории множеств, напротив, если ваш пакет лежит в какой-то сумке, то помидоры могут остаться внутри пакета и одновременно быть снаружи сумки. 

На самом деле тут нет ничего противоестественного, и следуя, например, фразе Б. Рассела о том, что множество вилок само вилкой не является, можно быстро понять почему в этом нарушении транзитивности нет противоречий. Действительно, когда мы начинаем рассматривать не только содержимое, но и содержащее, не только объекты, отграниченные друг от друга, но и сами границы рассматривать как объекты, то совершенно не обязательно, чтобы эти два объекта (содержимое и содержащее) находились бы в одном и том же классе, ну или были бы объектами одного и того же рода. 

Немного поговорим еще об одном значке из теории множеств, ну или еще об одном отношении между множествами, которое пишут следующим образом²: 

A ⊂ B

Это читают как то, что множество А является уже не элементом, но подмножеством множества B, и говорят, что А включено в B. 

Эти отношения в некотором смысле дуальны к отношениям принадлежности, потому что в случае отношений принадлежности А является элементом B, но содержимого А это не касается, так как те, кто являются элементами А не обязаны быть элементами B. Здесь, в случае знака “⊂” получается наоборот: элементы А являются элементами B, но само А это не касается, оно может вполне располагаться снаружи B.

Формально определить отношения включения A⊂ B можно следующим образом: 

∀x (x∈A) => (x∈B)

Эта запись означает, что, какой бы х вы не взяли, если он принадлежит А, то он принадлежит B. Можно чуть менее формально говорить, что А является частью B, имея в виду, что состоит из части его элементов. Опять же отметим, что самого А (как объекта) это не касается, то есть оно вполне может находиться снаружи той сумки в которой находится его содержимое³. 

Резюмируем отличия отношений принадлежности “A∈B” и включения “A⊂B” на диаграмме:

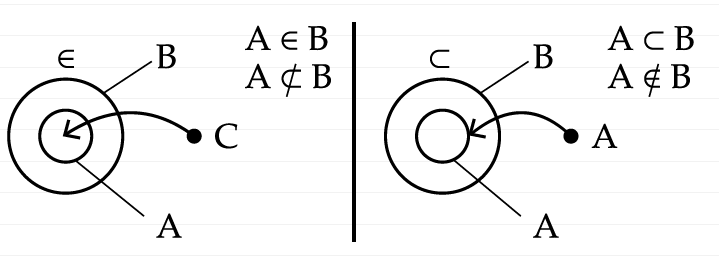
Слева иллюстрация отношений принадлежности: множество A принадлежит множеству B, но элементы множества А, то есть C, не обязательно принадлежат B, поэтому C в виде точки нарисовали снаружи B, стрелкой показав, его связь с A. Таким образом, в данном случае А является элементом B, но не является его подмножеством. Справа иллюстрация отношений включения, в которой все происходит дуально: Элементы A находятся внутри B, но само A расположено снаружи.

Итак, множества — необычные сумки, которые устроены скорее как диаграмма инь\янь, чем как концентрические круги силлогизмов Аристотеля. И, как мы и сказали, первый шаг в теорию множеств можно понимать, как возникновение границы между вещами в качестве вещи. В этом смысле теория Кантора — это математический язык, на который можно перевести то, как практика китайской живописи,  опирающаяся на Дао Дэ Цзин, делает своим объектом пустоту или может обозначить вещь, не рисуя ее, но рисуя границу между ней и другими вещами. Что касается дискурса психоаналитического, то тут можно найти огромное число применений этой канторовской логики. К примеру, чуть более ясным с точки зрения множеств, может стать “децентрация” субъекта по отношению к своему полу, которую описывает Э. Джонс. В его работе о развитии женской сексуальности свой собственный пол субъект обнаруживает в другом теле. Эту логику развивает и Джоан Ривьер, когда говорит про то, как этот свой пол ты носишь в качестве маски, то есть, возникая в качестве кого-то другого. Как можно было убедиться из этой части текста, такое необычное расположение вполне схватывается отношениями принадлежности или дуальными к ним отношениями включения.  

Кантор и Маркс

Идея обратиться к теории множеств в связи с понятием прибавочной стоимости появилась из текста Маркса. В одном из пассажей, призванных ввести это понятие, он в свойственной ему остроумной манере критикует понятие стоимости труда. В общих чертах эта история звучит так: За 12 часовой рабочий день рабочему платят какую-то сумму. Известно, что труд и есть то, что производит стоимость, иными словами стоимость можно измерять часами труда. Тогда вопрос о том сколько стоят 12 часов труда, звучит примерно так: “Сколько часов труда содержится в 12 часах труда?”. Учитывая, что рабочему платят меньше, чем стоимость, которую он за эти 12 часов производит, получается, что в 12 часах труда будто бы содержится меньше, чем 12 часов труда… 

В этом месте мы можем заметить, что речь идет об определенных отношениях содержимого и содержащего, которые выглядят странно и даже парадоксально. Что-то не так с этим рабочим днем, который состоит из 12 часов, но если узнать, сколько часов в 12 часах, то их окажется, к примеру, 6. Эта странная разница — между числом часов в рабочем дне и числом часов, содержащихся в часах рабочего дня — и определяет величину прибавочной стоимости. Не снимая парадоксальности происходящего, можно записать прибавочную стоимость (обозначим ее буквой а) следующим образом:

а = (часы, из которых состоит рабочий день  –  часы, из которых состоят часы, из которых состоит рабочий день).

или чуть в другой формулировке:

а = (часы как содержимое – часы как содержащее)

В самом деле, сначала говорится о часах, которые содержатся в рабочем дне, таким образом, речь о содержимом. Потом говорится о часах, которые содержатся в 12 часах рабочего дня, и таким образом часы рабочего дня начинают функционировать как содержащее. 

Исходя из этого кажется возможным понять, почему теория множеств может стать письмом для подобных, на первый взгляд паралогических, объектов. Собственно, чтобы убедиться в этом, можно вспомнить одну лишь на первый взгляд достаточно не логичную историю, которая порой возникает в учебниках в качестве простой задачки на понимание вводных понятий этой теории. Речь идет о вопросах, где нужно сказать, сколько элементов в множестве. Мы будем изображать множества, как и его элементы, окружностями, которые таким образом и сами являются множествами. Итак, вот пример вопроса о том, из скольких элементов состоит множество:

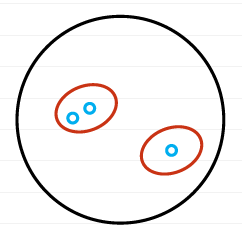
Черная окружность — это множество, про которое был поставлен вопрос. В нем мы обнаруживаем красные окружности, в которых находятся синие окружности. Если бы мы думали про множества как про сумки, то синие кружки — это то, что лежит в красных сумках, которые лежат в черной сумке. Тогда мы бы сказали, что в черной сумке находится 5 окружностей. Однако, такой ответ не является верным. Множество, которое символизировано черной окружностью состоит только из двух элементов, а именно, из двух красных кругов. Как мы уже сказали в прошлой части, транзитивность не обязательное свойство отношений принадлежности, поэтому строго говоря воображать множества сумками не слишком корректно. Множества — это необычные сумки. 

При этом в  учебниках по азам теории множеств можно прочесть, что множество задано своими элементами. Можно сказать, что оно произведено или определено ими. Подобно тому, как стоимость того или иного рабочего дня определена через количество часов, которые в нем содержатся. 

Хорошо, тогда зададимся следующим, уместным для нашего контекста, вопросом: Множество задано, ну или определено своими элементами, но чем заданы его элементы? 

В нашем примере, множество задано красными окружностями, которые сами заданы синими окружностями. Другими словами, синие окружности мы потратили на производство красных окружностей, которые произвели черную окружность. Красные окружности таким образом выступают и как содержащее и как содержимое, и  в этом смысле они и подобны парадоксальным часам рабочего дня пролетария. Эти часы и содержатся в рабочем дне, стоит сосчитать их и получим стоимость, которую пролетарий отдаст, но и сами они работают как содержимое, так как состоят из стоимости, которую пролетарий получит. 

Попробуем постепенно начинать говорить чуть более формально. По одной из аксиом теории множеств Цермело-Френкеля (аксиома множества суммы⁴) мы можем иметь множество, которое состоит из всех синих окружностей нашего примера. Тогда, если черную окружность мы назовем А, то множество синих будет называться UA:

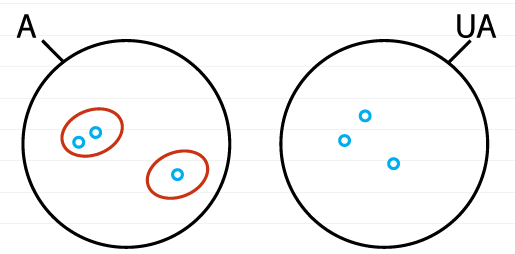
Множество UA состоит из элементов, из которых состоят элементы множества А. Другими словами, мы можем сказать, что элементы А — это те или иные подмножества множества UA. Опять же, для наглядности приведем еще один рисунок, где синие окружности заменим на разные буквы:

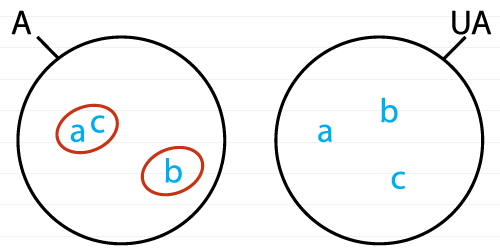
Здесь множество UA — это множество из трех букв, его можно записать как {a,b,c}. В данном примере элементы А являются двумя подмножествами множества этих букв: {a,c}, {b}. В предельном, ну или в максимальном, случае элементами множества А будут все возможные подмножества множества UA. Если множество состоит из n элементов, то множество всех его подмножеств будет состоять 2ⁿ элементов⁵. В данном случае их могло бы быть 2³ = 8. Таким образом, А было бы следующим множеством: {{a},{b},{c}, {a,b}, {a,c}, {b,c}, {a,b,c}, ∅}. Как мы видим, потенциально в А содержится больше, а иногда и гораздо больше, элементов, чем в UA. В предельном случае разница между А и UA равна (2ⁿ — n). 

Если перевести это на язык Маркса, то в этом предельном случае А можно рассматривать как рабочий день, состоящий из 2ⁿ рабочих часов, тогда как количество часов в этих часах будет равно n. В нашем примере, если рассматривать максимальную разницу, то мы получим, что рабочий день длится 2³ = 8 часов, но эти 8 часов состоят из 3 часов. В этой вариации капиталист отдает пролетарию стоимость 3, а получает стоимость 8, другими словами, величина прибавочной стоимости а= 8-3 = 5 часов. Пять часов труда рабочего, как сказал бы Маркс, достались капиталисту в подарок, ну или остались не оплаченными. 

Дискурс, благодаря Марксу, мы можем понимать как тип социальных связей, который можно мыслить как обмен, но обмен в котором кто-то дает больше, чем получает взамен. Неравноценный обмен капиталистического дискурса можно попробовать записать через отношения между двумя множествами. Для этого мы воспользуемся отношениями, которые пишутся знаком “⊂”. Например, пусть имеются два множества А и B, и при этом A⊂B. Это значит, что А является подмножеством B, ну или что любой элемент А одновременно является элементом B. Можно сказать, что А состоит из части элементов B. 

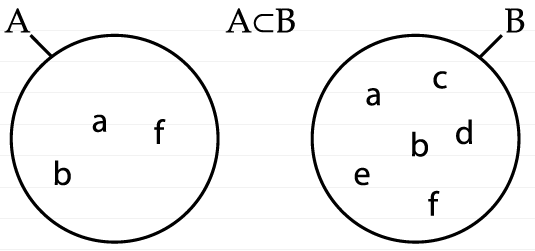
Множество B состоит из элементов а, b, c, d, e, f, тогда как множество А состоит из части этих элементов, а именно из а, b, f.  

Не формально отношения теории множеств можно интерпретировать разным образом, как например, в парадоксе Рассела отношения принадлежности x∈y, интерпретируются как “y бреет х”. Другими словами, сами по себе они бессмысленны, и читать их можно любым способом, лишь бы этот способ не нарушал логику использования этих отношений. В нашем случае, знак включения “⊂”, A⊂B, который мы поняли как А состоит из части элементов B, мы можем также понимать через обмен: B предоставило А его элементы, ну или эти элементы можно мыслить как стоимости, которые B дало А. Опять же, для наглядности, эту неформальную интерпретацию на диаграмме будем изображать стрелочками:

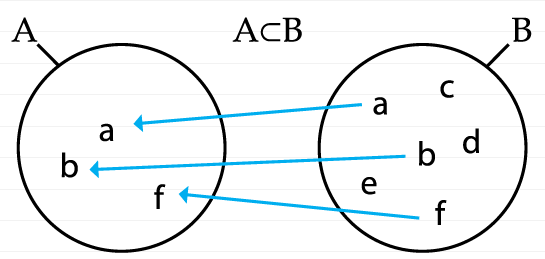
Они нужны только чтобы подчеркнуть способ читать эти отношения, то есть, что B передает А определенные стоимости, ну или оплачивает их. В данном примере B “оплатило” все элементы, из которых состоит А. 

Еще раз повторим вопрос капиталистического дискурса в его первоначальной парадоксальной форме: “Сколько часов труда в 12-часовом рабочем дне?”. Неравноценность обмена в том, что в 12 часах труда оказывается меньше часов труда, чем 12. Капиталист платит, таким образом, не за 12 часов труда, а за те часы труда, которые содержатся в этих 12 часах труда. Исходя из этого, мы можем записать первый такт обмена между множествами A и B. Пусть B “платит” А, как капиталист платит за рабочий день, но платит не за то, из чего состоит А, то есть не за его элементы, а за то, что эти элементы содержат. То есть, если А — это рабочий день, то будут оплачены не его часы, а часы, из которых состоят его часы. Это значит, что элементы элементов А будут частью элементов B: 

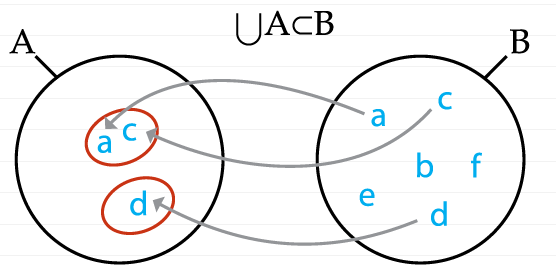
Таким образом, в данном случае множество сумма UA является подмножеством B: UA⊂B. 
Таким образом, мы записали шаг обмена, на котором капиталист отдает число часов труда, которые содержатся в 12 часовом рабочем дне. Отдав их, он что-то забирает, а именно, те стоимости, которые производит пролетарий. Другими словами, ему достанется стоимость, возникшая за день труда, которая эквивалентна 12 часам. Он отдает стоимость, равную числу часов, содержащихся в часах рабочего дня, и при этом забирает стоимость, равную числу часов в рабочем дне. Тогда в нашей записи, получается, что от А к B должны перейти элементы А. Другими словами, множество B возникает как часть множества А:

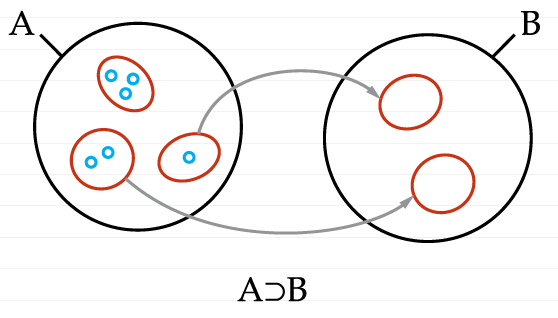
Таким образом, если совместить два такта обмена, то получим следующие отношения между А и B: 

UA ⊂ B

  A  ⊃ B

Элементы элементов А являются частью элементов B. Элементы B являются частью элементов А.
Схематично нарисуем сразу оба шага, и таким образом придем к диаграмме капиталистического обмена:

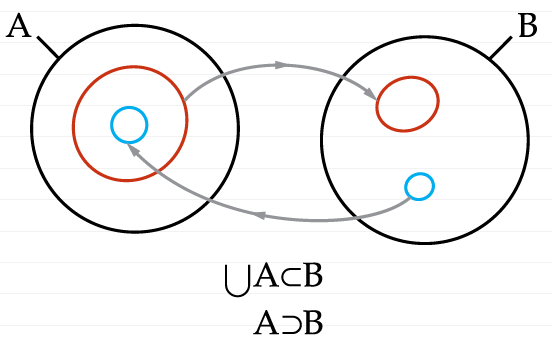
Мы свели то, что находится в А только к двум окружностям, чтобы не загромождать рисунок, и сделать нагляднее саму структуру. По ходу дела можно  заметить примечательную деталь, что две окружности в B находятся рядом друг с другом, то есть являются элементами B, тогда как в А синяя находится внутри красной. Таким образом, мы получили искомую запись неравноценного обмена: А можно сравнить с рабочим днем, который состоит из красных окружностей (часов), они “достанутся” B, тогда как А “достанется” то, что содержится в этих красных окружностях, то есть то, что парадоксальным образом было озвучено Марксом  в виде вопросов из серии: сколько часов в 12 часах? или сколько метров в одном метре? и т.п. Другими словами, то, что станет количеством труда, которое нужно для производства самого пролетария, то есть для воспроизводства его способности трудиться, а не то, в каком количестве часов труда эта способность реализуется. Получившаяся диаграмма отличается от того как можно было бы нарисовать симметричный обмен, где я тебе даю одно, а ты мне даешь другое. Последнюю можно было бы примерно вообразить так:

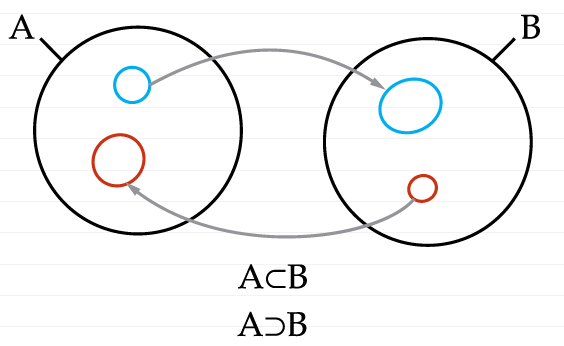
В этом случае множества А и B просто совпадут, то есть будут состоять из одинаковых элементов. В случае диаграммы капиталистического обмена появляется асимметрия, которая позволяет подсчитать прибавочную стоимость.
Прежде чем написать ее подсчет, запишем два такта обмена в линию, тогда выглядеть он будет так:

 UA ⊂ B ⊂ A

Из этого следует, что UA ⊂ A. Это значит, что UA состоит из тех же элементов, что и само А, является его частью. В целом, можно оставить ситуацию в таком виде⁶, либо просто избежать этой избыточной  самореференции. Для этого, мы на втором шаге, внесем ограничение и скажем, что только та часть B является подмножестом (частью) А, которая не совпадает с UA. Записать эту часть B можно, например так: B/UA, ну и соответственно второй такт обмена будет записан так: (B/UA) ⊂ A.

Эта поправка будет значить в нашей интерпретации, что B отдает UA, а получает не то, что отдает, то есть, в нашем случае, получает элементы А.

Когда мы пишем два такта обмена в линию, то приходим к версии записи капиталистического дискурса, которая в самом простом виде пишется так: 

Д-Т-Д

Перед нами также два обмена: деньги, потом их меняют на товар, который в данном случае связан с трудом, а потом взамен получаются новые деньги. В средней части происходит расщепление, так как труд разделяется на тот, который производит рабочего и тот, который производит рабочий. Имеет место то, что можно сопоставить с понятием расщепленного субъекта у Лакана, и то, что мы пишем с помощью дихотомии содержимое\содержащее. Благодаря этому мы можем представить нашу запись в форме близкой к той, которую пишет Маркс, но на другом языке: 

B  ⊃  UA, A  ⊃  (B/UA)

На втором такте также происходит расщепление на А и UA, то есть элементы множества А задействованы то как собственно элементы, то есть содержимое А, то как содержащее, то есть то, что само состоит из элементов UA. В этой записи в первом обмене B что-то отдает, а именно элементы UA, а потом что-то получает, а именно элементы А. 

Опять же повторим, что на последнем такте, когда мы пишем B/UA,
которое создается как часть А,  то тем самым мы пишем, что только та часть B является подмножеством А, то есть, состоит из его элементов, которая не состоит из содержимого самих элементов А. Это то, что B получает от А, отдавая ему UA.

Величина прибавочной стоимости может быть тогда подсчитана как разница между этими двумя частями множества B. 

|a| = |B/UA| — |UA|

Мы пишем названия множеств как числа по модулю, чтобы обозначить, что речь идет именно о количестве элементов. 

Итак, теория множеств дает версию записи капиталистического неравноценного обмена. Еще раз представим этот капиталистический инь\янь в простой схематичной форме:

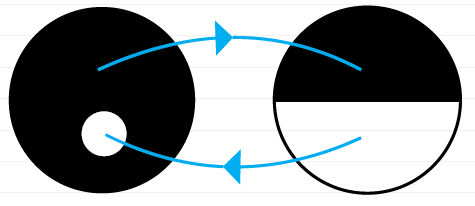
Маркс и Лакан

Что касается Лакана, то он, конечно, был из тех, кто пользовался мыслью Маркса. Например, в 16 семинаре это происходит совершенно явным образом. При этом среди основных его понятий явным образом возникает прибавочное наслаждение. В некотором смысле интенцию Лакана можно было бы назвать попыткой к обобщению. Прибавочное наслаждение — это попытка сказать про что-то в более общем виде, но этот более общий вид дает возможность задуматься о чем-то более частном, чем отношения между классом капиталистов классом пролетариев. В более общем виде мы можем сказать, что эксплуатация, неравноценность обмена, отчуждение — это не только структура, которой можно охарактеризовать производственные отношения. Благодаря Лакану, мы начинаем понимать, что в общей формулировке проблема состоит в отношениях с означающим, ну или, можно сказать, в отношениях с речью. Но тогда возникает и более частное, так как проблема в отношениях с означающим реализуется на уровне конкретного субъекта, ну или, если говорить более перформативно, реализует его. Короче говоря, в рамках этого обобщающего хода, тем не менее, можно начинать думать о решениях, которые являются не такими общими, как “мировая революция”, которая порой кажется единственным лекарством от капиталистического дискурса.  Проект такой практики, ну или такого взгляда на психоаналитический дискурс, можно расслышать в одном из ответов Лакан из текста “Телевидение”:  “Ça pourrait être la sortie du discours capitaliste, mais ça ne constituera pas un progrès si ça ne se passe que pour certains”. В любом случае к этому взгляду на практику анализа стоит подходить осторожно, так как можно случайно соскользнуть в такую разновидность идеализма, которая хочет вернуть все проблемы внутреннему миру субъекта, игнорируя, известный всем переворот гегелевской фразы, который сделал Маркс, сказав, что бытие определяет сознание, а не наоборот.  Возможно, этого ляпа удается избежать, в силу того, что все лаканисты знают, что означающее определяет субъекта, что он от него принципиально зависим. 

В этой части мы посмотрим формулу из текста Лакана, который не содержит эксплицитной ссылки на Маркса, тем не менее его логика совершенно идентична логике неравноценного обмена капиталистического дискурса. Для этого сначала, запишем еще одну вариацию определения прибавочной стоимости через вычитание. 

Ее помогает записать разделение стоимости на меновую и потребительную. Это разделение стоимости на две гетерогенные ну или не сопоставимые вещи, трансформируется в случае рынка труда, потому как покупка и потребление рабочей силы позволяют вычесть одно гетерогенное из другого. Возможность купить рабочую силу подразумевает наличие у нее меновой стоимости, но и ее потребление или ее потребительная стоимость, реализуется в образовании новой меновой стоимости. Поэтому можно записать прибавочную стоимость так:

прибавочная = потребительная — меновая

, эта формула, как мы и сказали, перестает быть чем-то противоречивым только в условиях особого объекта (рабочей силы) чьи стоимости тут вычитаются. Расщепление “субъекта-пролетария” мы уже описали в предыдущей части, и выражается оно, к примеру, в том, что платят ему за его способность трудиться, за его присутствие на рабочем месте, а не за то, что он, присутствуя, создает. Слово присутствие мы употребляем здесь, чтобы перейти к формуле Лакана из текста “Значение фаллоса”:

 желание = потребность — требование

Конечно, эта формула выглядит несколько странно, когда видишь ее впервые, именно потому что она вычитает друг из друга две, казалось бы, гетерогенные вещи. С другой стороны, эта гетерогенность исчезает по ходу чтения текста Лакана и позволяет утверждать, что перед нами вариация сказанного Марксом. 

Лакан начинает с того, что у субъекта есть потребность и есть Другой, который может дать объект, ее удовлетворяющий. На самом деле, эти потребности тут можно понимать в широком смысле, просто как объект, который дает то или иное удовлетворение. 

Тогда возникает обращение к этому Другому, ну или требование. Лакан в этом тексте делает упор на то, что у любого требования есть “обратная сторона” быть требованием присутствия. По сути это означает выход требования во второй порядок, потому что сначала вы требуете от Другого объект, который он может дать, а потом требуете само присутствие этого Другого. Второй порядок возникает аналогично тому как это происходит в логике, когда сначала вы говорите что-то про содержимое класса, про его индивидов, ну или объекты, а потом про само содержащее, про сам этот класс. Короче говоря, можно сказать, что в ряду объектов появляется такой объект как “присутствие”, назовем его объектом второго порядка.

В чем, если так можно выразиться, побочный эффект этого требования присутствия? На самом деле, этот эффект состоит в обесценивании первопорядковых объектов. Почему? Потому, что объект, каким бы он ни был, перестает в чистом виде интересовать как объект удовлетворяющий потребность, но разве что в качестве знака присутствия Другого. Таким образом, как скажет Лакан, часть потребности, теряется за требованием присутствия. 

Отсюда возникает его формула, так как эта обесцененная часть и станет объектом желания, то есть, она формируется из остатка вычитания требования из потребности:

желание = потребность — требование

Подчеркнем, что в истории про требование присутствия удобно мыслить происходящее в терминах содержимого и содержащего. В силу того, что Другой предоставляет объекты, удовлетворяющие потребность, его можно сравнить с содержащим, а эти объекты с содержимым. Тогда на втором витке, то есть, когда требование становится не требованием объекта, а требованием присутствия этого Другого, то содержащее само выступает в качестве объекта, то есть в роли того, что имело отношение к содержимому. Отсюда мы получаем прямую связь исследуемой формулы, с тем, что в прошлой части говорили про капиталистический обмен. В тексте Лакана, как и в прошлой части, всё сводится к разнице между содержимым и содержащим. Эту разницу обозначим маленькой буквой а, и запишем: 

a = содержимое — содержащее

Если смотреть на эту часть в связи с речью, ну или в связи с “материей”, в которой сформулировано требование, то есть, в связи с означающим, то отсюда можно заключить, что желание будет высказываться там, где требование “умолкает”, скорее в его разрывах, ну или что означающее всегда имеет возможность сказать больше, чем намеревалось, в силу его двусмысленностей, переносного смысла и т.п. Эти экивоки — единственный способ высказать то, что теряется в связи с требованием. Понятно, почему Лакан инвертирует характеристики требования присутствия, которое он еще называет требованием любви. Если требование любви имеет некоторые свойства, то желание должно иметь обратные свойства как раз потому, что оно связано с тем, что требование присутствия обесценивает, а значит желание имеет отношение к тому, что этому требованию любви противоположно. Отсюда он в частности переходит от “безусловного требования любви” к “абсолютному условию желания”. Отсюда же рождаются эти лакановские формулы в духе Дао Дэ Цзин, что желание артикулировано тем, что артикуляции не поддается, ну или обращение к промежутку между означающими, подобное тому как задействуется в китайской живописи промежуток между вещами. 

Записывая такты лакановской трансформации в строку, мы приходим к следующему:

П -> Т -> П´

, где П означает потребность, Т — требование,  а П´ — это, что случается с потребностью после артикуляции в требовании, а именно обесценивание ее части. Это событие происходит, в силу того, что на уровне Т имеет расщепление между требованием объекта и требованием присутствия, ну или любви. 

Психоанализ и Топология

Различия, которые мы рассматривали в этом тексте, и особенно подход к различию между содержимым и содержащим, достаточно удобно иллюстрировать примерами из области интуитивной топологии. Наглядность топологических объектов привлекала не только Лакана, но и Леви-Стросса, тексты которого являются одним из лучших объяснений того, как в чем-то скорее гуманитарном, вроде антропологии, полезно прибегать к чему-то скорее математическому, вроде топологии. Собственно, и для нашего рассмотрения отношений из книги Капитал или формулы из статьи “Значение фаллоса” в этой области можно найти очень красивые иллюстрации. Приведем пример такого рисунка из книги математика Л. Кауфмана:

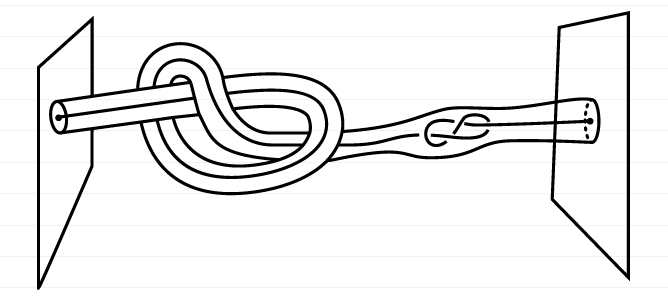
В данном случае, узел выступает не только как содержащееся в некотором пространстве, но и как содержимое для другого узла. При этом другой узел, узел, расположенный в первом узле, с одной стороны его повторяет (слева), а с другой (справа) просто находится внутри. Таким образом, содержимое повторяет содержащее, но не полностью. На этой разнице узла как содержимого от узла как содержащего другой узел строится одно доказательство о свойствах композиции узлов. Для нашего же случая мы получаем еще одну замечательную иллюстрацию, к примеру, для разницы между потребностью и требованием или и т.п., о которых написали выше. 

С другой стороны, переход к топологии возникает в самой теории множеств. В первых двух главах книги Nons Ж.М. Вапперо начинает говорить о введении в логику достаточно необычным способом, а именно, через теоретико-множественную топологию. И если продолжить немного наш дискурс о различиях, то топология предстает тем, что делает еще один шаг в этом движении: Аристотель, Кантор и далее. В нашем изложении мир Аристотеля — это мир, где вещи классифицированы, разложены по разным местам (внутри\снаружи), в мире Кантора сами классы возникают как объекты, ну или, как мы сказали, сами границы между вещами предстают как вещи. 

В этом смысле можно понимать множества по аналогии с тем как Лакан мыслил означающие, например, понимая их как купюры, ну или разрезы. Снова обращаясь к китайскому пейзажу, мы можем напомнить его типичную структуру, о которой можно прочесть в книге Ф. Чанга о функции пустоты в китайской живописи. Типичный пейзаж — это небо, снизу горы, но между ними полоска тумана, который символизирует пустоту, отделяющую инь от янь. Нужно отметить, что туман, будучи пустотой — это не совсем отсутствие границы, но это скорее то, что обозначает ее нехватку в условиях, когда удалось ее рассмотреть как объект наряду с другими. Тогда, как только мы поняли множество как означающее различия, ну или как возникновение в качестве объекта границы между различными объектами, то мы можем говорить и о нехватке этой границы. Но именно так мы неформально можем представить шаг в область топологии. В ней появляется новое различие, так как множества можно разделить на открытые и закрытые. Открытые можно писать круглыми скобками (), а закрытые квадратными []. Одни говорят о совокупностях имеющих край, а другие о тех, у которых его нет. Короче говоря, еще раз заметим, что там, где промежуток между объектами сам становится объектом, может иметь место и его нехватка, которую в лакановской алгебре обычно пишут как означающее нехватки означающего S(A\).

to be continued

1. Это различие можно обозначать парой интренсек\экстренсек. Переход от интренсек к экстренсек — это не переход от внутри к снаружи, но переход от рассмотрения объекта самого по себе к его внешнему рассмотрению, к его рассмотрению в контексте некоторого пространства, в котором он расположен. ↩︎
2. Для введения теории множеств достаточно было бы пользоваться одним из этих знаков, а второй рассматривать как аббревиатуру. Тем не менее мы вводим второй знак для наглядности, а также, потому что будем им пользоваться в части про Маркса. ↩︎
3. При этом отношения включения транзитивны, это значит, что если (A⊂ B) ⋀ (B⊂C), то (A⊂C). Это становится очевидным, если иметь в виду определение отношений включения. В самом деле, если содержимое А лежит внутри B, то оно является содержимым B. И если B включено в С, то все содержимое B лежит в С, в том числе содержимое А, а значит А является подмножеством С. Поэтому аксиомы силлогизмов Аристотеля, можно было перевести на язык теории множеств именно через отношения включения. То, что в логике мы определяли через “находиться внутри” теперь можно переопределить через “быть подмножеством”. 
   Однако, еще раз на всякий случай повторимся, что речь идет именно об элементах множества А, но не о нём самом. Другими словами, хотя отношения включения так же можно рисовать окружностями внутри других окружностей, но сами эти окружности не обязательно находятся внутри того, что находится внутри них. 
   ↩︎
4. Теория Цермелло-Френкеля является самой популярной версией теории множеств, которой пользуются в наши дни в математике. ↩︎
5. Эту формулу Кантора мы приводим без доказательств, чтобы избежать излишних подробностей. ↩︎
6. На семинаре на переулке Сивцев-Вражек, мы не вводили дополнительных ограничений, другими словами, оставляли эту связь А с самим собой. Однако, впоследствии стало понятно, что можно действовать немного по-другому, и здесь мы будем идти именно этим путем. ↩︎