---

Текст:

Здравствуйте.

Ну как бы у Александра Сергеевича есть замечательная такая конструкция в Послесловии у Узлу — там он развивает идею Лакана / Вапперо о том, чтобы рассматривать точку как трискель¹.

Ну это оммаж к ней.

Ну мы будем выражаться емко, ибо наглядно.

Как слева от нас.

Есть современный раздел математики — инконсистентные геометрии (фундаментом которых являются паранепротиворечивые и параполные теории множеств)².

Это область наполнена т. н. невозможными фигурами, частным случаем которых является трибар Пенроуза.

Когда Лакан спустя сто лет отвечает

Jiun SONJA, Ce qui veut dire: «Dans trois mille ans, combien d’hommes sauront?»

LACAN, Je me suis permis, dans ma propre calligraphie, de répondre: [рис. 1]³ он, де-факто, использует инконсистентную конструкцию — натяните ткань не отрывая фигуру от листа.

Любом случае понадобится перемычка, ребро между внутренним и внешним оборотами, чтобы изъять ее в R3.

Когда Бронников обращается к картине Орхидея, бамбук, камень китайского живописца Шитао⁴, он также имеет дело с инконсистентной конструкцией.

Здесь зайти через разрезанную бутылку Клейна.

В общем случае, скрут оказывается тесно связан с порядком линий, который организует пустоту,

разрыв, анаморфозу.

Обратите внимание, как оказываются соположены регистры воображаемого и символического, как они вторят друг другу:

зелубой и картина Шитао, заяц-утка и, например, здразвиданья.

Когда S и I столь тесно переплетены, речь идет о логике фантазма?

кросс-кэпе? Как организована пустота в узле Уайтхеда?

Это открытый вопрос, который мы встретим еще не раз, в частности, в экзистенциальных графах Пирса.

Я пишу тебе на лоб: «шем»

Хрестоматийным примером такой инконсистентной конструкции является трибар Пенроуза.

Фокусы

Сначала сама конструкция точка — трискель

Затем заменяем три точки схождения трех плоскостей трибара на скруты. Выделяем край, получаем узел трефль.

Ну затянем его, будет одна точка схода.

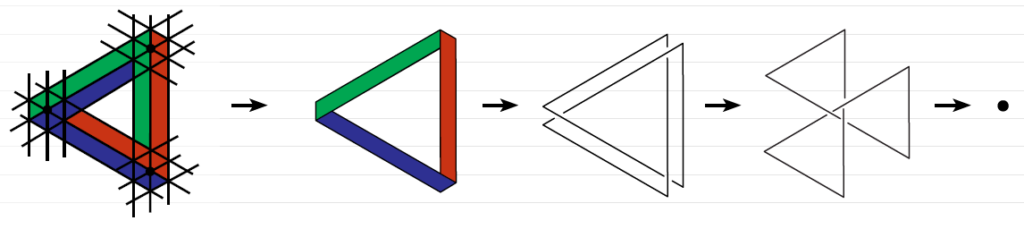
Иначе, разведем плос’кости трибара

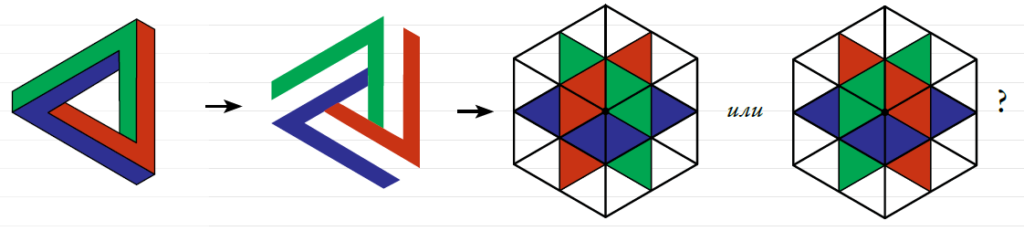
Получаем декартов куб. Кстати говоря, Лакан показывает такой фокус

Это — полиэдрическая модель римской поверхности Штейнера, тетрагемигексаэдр, проективный многогранник, звездчатый до бесконечности. Его можно получить из тетраэдра через обобщенную операцию усечения (troncation).

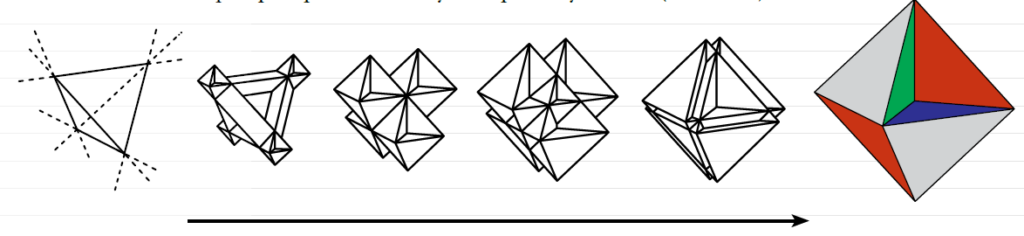
Troncature généralisée des arêtes et des sommets du tétraèdre. https://mathcurve.com/polyedres/chanfreine/chanfreine.shtml

Поверхность Штейнера, в свою очередь, связана с плоскостью Фано, а плоскость Фано, с группой PSL (3,2). Которая, в свою очередь, как об этом уже сказал Гитар, с группой G₁₆₈,

И Борромеевой узлоцепочкой.

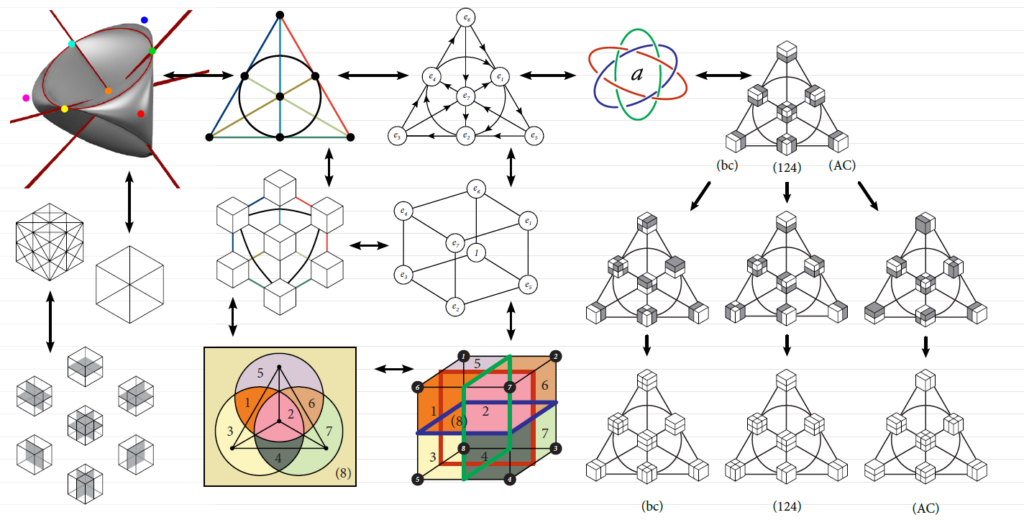
В заключение, ответ Жану-Мишелю, с его указаниями⁵,

Заниматься непрерывными отображениями, прерывными не заниматься⁶. Не переопределять импликацию в каждой работе, не заниматься ультрафильтрами⁷, не порождать больше Лаканов и Фрейдов⁸ и т.д.

Литералли ни одно предостережение не сработало

Ответ-привет

Nons.

ceci Moi parlettre

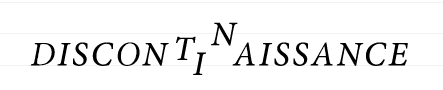
1. С ее помощью легко перевести матему дискурса из графа в узел Bo. ↩︎
2. Chris Mortensen. Inconsistent Geometry (Studies in Logic).
   Inconsistent Mathematics (Mathematics and Its Applications, 312) 1995th Edition. ↩︎
3. 15 Décembre 1965 13 Sem. ↩︎
4. Orchids, bamboo, rock. Shitao (Zhu Ruoji). 1656 — 1707. Ink and wash painting. 72.5 x 51 cm ↩︎
5. Ткань. с. XV
   Там же. «Сшивание места субъекта отныне завершено». Не, субъекта ждет импликация
   в мир
   Там же. «за дело берется Канробер». Так себе берется.
   Там же. «Наших тетрадей шесть». Нет, семь.
   И Т.Д. ↩︎
6. Ну вот, трибар. ↩︎
7. На ультрафильтры хорошо ловить логиков и аналитических философов. ↩︎
8. Поставить их производство на поток. ↩︎